絶対値を外す基本的な方法は既に学習した。(不安な人はこちら⇒絶対値とその性質)ここでは、方程式や不等式にこの絶対値が含まれる場合にどのように解いていけばよいかを見ていく。
絶対値を含む方程式と不等式の解き方
基本解法
絶対値を含む方程式・不等式を解く手順は、以下に示すものが基本となる。
[方程式]
[1] 場合分けにより、絶対値を外す。
$\begin{eqnarray} \textcolor{hotpink}{|X|}= \begin{cases} \textcolor{hotpink}{X} & (\textcolor{cornflowerblue}{X\geqq 0})\\ \textcolor{hotpink}{-X} & (\textcolor{cornflowerblue}{X\lt 0}) \end{cases} \end{eqnarray}$
[2] 各場合ごとに得られた方程式を解く。
[3] 得られた解が、場合分けの条件を満たしているかを確認する。
[4] 各場合の条件を満たした解をまとめて、最終的な解とする。
[不等式]
[1] 場合分けにより、絶対値を外す。
[2] 各場合ごとに得られた不等式を解く。
[3] 得られた解(範囲)が、場合分けの条件を満たしているかを確認する。
[4] 各場合の条件を満たした解(範囲)をまとめて、最終的な解(範囲)とする。
とはいえ、この手順ですべての問題を考えるのは手間である。実は、ある特定の場合にはスパッと瞬殺できてしまうので、以下で紹介していく。
場合分けを省略できる(瞬殺可能)なパターン
方程式・不等式が絶対値を含む場合、中身の正負により場合分けをするのが基本であった。しかし、次のような場合には場合分けをせずに絶対値を外すことができる。
右辺が定数である場合
右辺が正の定数である不等式や方程式の場合、絶対値が原点からの距離を表していることを利用することで、場合分けせずに絶対値を外すことができる。
右辺定数型➀
$\begin{eqnarray} &\ &\textcolor{hotpink}{a\gt 0}のとき\\[5pt] &\ & \begin{cases} \textcolor{cornflowerblue}{|x|=a}&\Leftrightarrow &\textcolor{hotpink}{x=\pm a}\\ &&(\textcolor{limegreen}{原点からの距離}が\textcolor{hotpink}{aの場所})\\ \textcolor{cornflowerblue}{|x|\lt a}&\Leftrightarrow &\textcolor{hotpink}{-a\lt x\lt a}\\ &&(\textcolor{limegreen}{原点からの距離}が\textcolor{hotpink}{aより近い範囲})\\ \textcolor{cornflowerblue}{|x|\gt a}&\Leftrightarrow &\textcolor{hotpink}{x\lt -a,\ a\lt x}\\ &&(\textcolor{limegreen}{原点からの距離}が\textcolor{hotpink}{aより遠い範囲})\\ \end{cases} \end{eqnarray}$
数直線にしてみると以下のようになる。
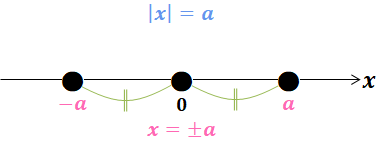
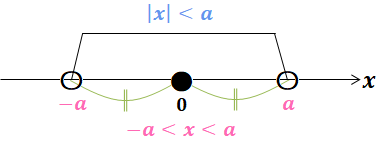
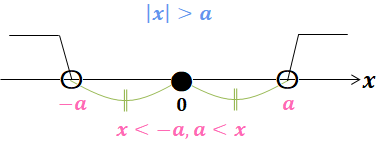
また、$a\leqq 0$ の場合を考えると、絶対値は原点からの距離なのだから、常に $|X|\geqq 0$ である。このことより、
右辺定数型➁
$\begin{eqnarray} &\ &\textcolor{hotpink}{a=0}のとき\\[5pt] &\ & \begin{cases} \textcolor{cornflowerblue}{|x|=a}&\Leftrightarrow &\textcolor{hotpink}{x=0}\\ \textcolor{cornflowerblue}{|x|\lt a}&\Leftrightarrow &\textcolor{hotpink}{xは存在しない}\\ &&(\textcolor{limegreen}{xに何を代入しても成り立たない})\\ \textcolor{cornflowerblue}{|x|\gt a}&\Leftrightarrow &\textcolor{hotpink}{0でないすべての実数}\\ &&(\textcolor{limegreen}{0以外であらばxに何を代入しても成り立つ})\\ \end{cases} \end{eqnarray}$
$\begin{eqnarray} &\ &\textcolor{hotpink}{a\lt 0}のとき\\[5pt] &\ & \begin{cases} \textcolor{cornflowerblue}{|x|=a}&\Leftrightarrow &\textcolor{hotpink}{xは存在しない}\\ &&(\textcolor{limegreen}{xに何を代入しても成り立たない})\\ \textcolor{cornflowerblue}{|x|\lt a}&\Leftrightarrow &\textcolor{hotpink}{xは存在しない}\\ &&(\textcolor{limegreen}{xに何を代入しても成り立たない})\\ \textcolor{cornflowerblue}{|x|\gt a}&\Leftrightarrow &\textcolor{hotpink}{すべての実数}\\ &&(\textcolor{limegreen}{xに何を代入しても成り立つ})\\ \end{cases} \end{eqnarray}$
である。学校では触れられないこともあるが、しっかりと確認しておいてほしい。
$|X|=|Y|$ 型・ $|X|\gt|Y|$ 型
この形は、場合分けによって求めることが基本とされているが、実は簡単に解くことができる。
使う知識は
[1] $\textcolor{hotpink}{|x|^2=x^2}$ (絶対値は2乗することで外せる)
[2] $a\geqq 0$, $b\geqq 0$ ならば、$\begin{cases} \textcolor{hotpink}{a=b}&\textcolor{hotpink}{\Leftrightarrow}&\textcolor{hotpink}{a^2=b^2}\\ \textcolor{hotpink}{a\gt b}&\textcolor{hotpink}{\Leftrightarrow}&\textcolor{hotpink}{a^2\gt b^2} \end{cases}$ (0以上の実数の大小関係は2乗しても変わらない)
という2つだけである。学校では習わないこともあるが、必ず覚えておきたい。
$|X|=|Y|$型
$\begin{eqnarray} \textcolor{palevioletred}{|x|=|y|}&\Leftrightarrow&|x|^2=|y|^2\\ &\Leftrightarrow&x^2=y^2\\ &\Leftrightarrow&x^2-y^2=0\\ &\Leftrightarrow&\textcolor{palevioletred}{x=\pm y} \end{eqnarray}$
$|X|\gt|Y|$型
※2次不等式の知識を必要とする。どうしてもよくわからない場合は、2次不等式学習後に見直してみてもらいたい。
$\begin{eqnarray} \textcolor{palevioletred}{|x|\gt|y|}&\Leftrightarrow&|x|^2\gt|y|^2\\ &\Leftrightarrow&\textcolor{palevioletred}{x^2\gt y^2}\\ &\Leftrightarrow&x^2-y^2\gt 0\\ &\Leftrightarrow&\textcolor{palevioletred}{(x+y)(x-y)\gt 0}\\ &\scriptsize{\textcolor{brown}{※}}&\scriptsize{\textcolor{brown}{x+y=A,\ x-y=B\ とすると、AB\gt 0\ のとき、}}\\ &\ &\scriptsize{\textcolor{brown}{A\gt 0\ かつB\gt 0\ か、A\lt 0\ かつB\lt 0である。}}\\ &\Leftrightarrow&\textcolor{palevioletred}{x\lt -y,\ y\lt x} \end{eqnarray}$
例題に挑戦しよう
≪問題≫
次の方程式、不等式を解け。
(1) $|x-4|=3$
(2) $|x-3|\leqq 6$
(3) $3|2x+2|-11\gt 7$
(4) $\left||x+1|-2\right|+3\geqq 4$
(5) $|x+2|=|x-5|$
(6) $|x-3|\lt |x-5|$
(7) $|x-3|=2x-5$
(8) $|2x-5|\leqq 4-x$
(9) $|x-4|\gt 5x$
(10) $2|x-1|+\sqrt{x^2+6x+9}\lt 7$
≪解答・解説≫
(1)※右辺定数型
$\begin{eqnarray} |x-4|=3 &\Leftrightarrow &x-4=\pm 3\\[3pt] &\Leftrightarrow &x=4\pm 3\\[3pt] &\Leftrightarrow &\boldsymbol{x=7,\ 1} \end{eqnarray}$
(2)※右辺定数型
$\begin{eqnarray} |x-3|\leqq 6 &\Leftrightarrow &-6\leqq x-3\leqq 6\\[3pt] &\Leftrightarrow &\boldsymbol{-3\leqq x\leqq 9} \end{eqnarray}$
(3)※移行し整理することで右辺定数型になる
$\begin{eqnarray} &\ &3|2x+2|-11\gt 7\\[3pt] &\Leftrightarrow &3|2x+2|\gt 18\\[3pt] &\Leftrightarrow &|2x+2|\gt 6\\[3pt] &\Leftrightarrow &2x+2\lt -6,\ 6\lt 2x+2\\[3pt] &\Leftrightarrow &2x\lt -8,\ 4\lt 2x\\[3pt] &\Leftrightarrow &\boldsymbol{x\lt -4,\ 2\lt x} \end{eqnarray}$
(4)※外側から順に絶対値を外していく。
$\begin{eqnarray} &\ &\left||x+1|-2\right|+3\geqq 4\\[3pt] &\Leftrightarrow &\left||x+1|-2\right|\geqq 1\\[3pt] &\Leftrightarrow &|x+1|-2\leqq -1,\ 1\leqq |x+1|-2\\[3pt] &\Leftrightarrow &|x+1|\leqq 1,\ 3\leqq |x+1|\\[3pt] &\Leftrightarrow &-1\leqq x+1\leqq 1,\ x+1\leqq -3,\ 3\leqq x+1\\[3pt] &\Leftrightarrow &\boldsymbol{x\leqq -4,\ -2\leqq x\leqq 0,\ 2\leqq x} \end{eqnarray}$
(5)※ $|X|=|Y|$ 型
$|x+2|=|x-5|$ より、$x+2=\pm(x-5)$
$x+2=x-5$ のとき、$0=-7$ となり不適
$x+2=-x+5$ のとき、$2x=3\ \Leftrightarrow x=\dfrac{3}{2}$
$\therefore$ $\boldsymbol{x=\dfrac{3}{2}}$
(6)※ $|X|\gt|Y|$ 型
$\begin{eqnarray} &\ &|x-3|\lt |x-5|\\[3pt] &\Leftrightarrow &|x-3|^2\lt |x-5|^2\\[3pt] &\Leftrightarrow &(x-5)^2-(x-3)^2\gt 0\\[3pt] &\Leftrightarrow &\{(x-5)-(x-3)\}\{(x-5)+(x-3)\}\gt 0\\[3pt] &\Leftrightarrow &-4(x-4)\gt 0\\[3pt] &\Leftrightarrow &x-4\lt 0\\[3pt] &\Leftrightarrow &\boldsymbol{x\lt 4} \end{eqnarray}$
(7)※基本解法の通りに場合分け
(ⅰ) $x-3\lt 0\Leftrightarrow x\lt 3$ のとき、
$\begin{eqnarray} &\ &|x-3|=2x-5\\[3pt] &\Leftrightarrow&-x+3=2x-5\\[3pt] &\Leftrightarrow&3x=8\\[3pt] &\Leftrightarrow&x=\dfrac{8}{3} \end{eqnarray}$
(ⅱ) $x-3\geqq 0\Leftrightarrow x\geqq 3$ のとき、
$\begin{eqnarray} &\ &|x-3|=2x-5\\[3pt] &\Leftrightarrow&x-3=2x-5\\[3pt] &\Leftrightarrow&x=2\quad(\ 2\lt 3\ より\textcolor{hotpink}{不適}) \end{eqnarray}$
$\therefore$ (ⅰ),(ⅱ)より $\boldsymbol{x=\dfrac{8}{3}}$
(8)※基本解法の通りに場合分け
(ⅰ) $2x-5\lt 0\Leftrightarrow x\lt \dfrac{5}{2}$ のとき、
$\begin{eqnarray} &\ &|2x-5|\leqq 4-x\\[3pt] &\Leftrightarrow&-2x+5\leqq 4-x\\[3pt] &\Leftrightarrow&1\leqq x\\[3pt] \end{eqnarray}$
よって、$1\leqq x\lt\dfrac{5}{2}$
(ⅱ) $2x-5\geqq 0\Leftrightarrow x\geqq \dfrac{5}{2}$ のとき、
$\begin{eqnarray} &\ &|2x-5|\leqq 4-x\\[3pt] &\Leftrightarrow&2x-5\leqq 4-x\\[3pt] &\Leftrightarrow&3x\leqq 9\\[3pt] &\Leftrightarrow&x\leqq 3 \end{eqnarray}$
よって、$\dfrac{5}{2}\leqq x\leqq 3$
$\therefore$ (ⅰ),(ⅱ)より $\boldsymbol{1\leqq x\leqq 3}$
(9)※基本解法の通りに場合分け
(ⅰ) $x-4\lt 0\Leftrightarrow x\lt 4$ のとき、
$\begin{eqnarray} &\ &|x-4|\gt 5x\\[3pt] &\Leftrightarrow&-x+4\gt 5x\\[3pt] &\Leftrightarrow&4\gt 6x\\[3pt] &\Leftrightarrow&x\lt\dfrac{2}{3} \end{eqnarray}$
(ⅱ) $x-4\geqq 0\Leftrightarrow x\geqq 4$ のとき、
$\begin{eqnarray} &\ &|x-4|\gt 5x\\[3pt] &\Leftrightarrow&x-4\gt 5x\\[3pt] &\Leftrightarrow&-4\gt 4x\\[3pt] &\Leftrightarrow&x\lt -1\quad(\ 4\leqq x\ を満たさず\textcolor{hotpink}{不適}) \end{eqnarray}$
$\therefore$ (ⅰ),(ⅱ)より $\boldsymbol{x\lt \dfrac{2}{3}}$
(10)※基本解法の通りに場合分け
$2|x-1|+\sqrt{x^2+6x+9}\lt 7\Leftrightarrow 2|x-1|+|x+3|\lt 7$より、
(ⅰ) $x-1\lt 0,\ x+3\lt 0\Leftrightarrow x\lt -3$ のとき、
$\begin{eqnarray} &\ &2|x-1|+\sqrt{x^2+6x+9}\lt 7\\[3pt] &\Leftrightarrow&-2(x-1)-(x+3)\lt 7\\[3pt] &\Leftrightarrow&-2x+2-x-3\lt 7\\[3pt] &\Leftrightarrow&-8\lt 3x\\[3pt] &\Leftrightarrow&-\dfrac{8}{3}\lt x\quad(\ x\lt -3\ を満たさず\textcolor{hotpink}{不適}) \end{eqnarray}$
(ⅱ) $x-1\lt 0,\ x+3\geqq 0\Leftrightarrow -3\leqq x\lt 1$ のとき、
$\begin{eqnarray} &\ &2|x-1|+\sqrt{x^2+6x+9}\lt 7\\[3pt] &\Leftrightarrow&-2(x-1)+(x+3)\lt 7\\[3pt] &\Leftrightarrow&-2\lt x\end{eqnarray}$
よって、$-2\lt x\lt 1\quad(\ -3\leqq x\lt 1\ との共通範囲) $
(ⅲ) $x-1\geqq 0,\ x+3\geqq 0\Leftrightarrow x\geqq 1$ のとき、
$\begin{eqnarray} &\ &2|x-1|+\sqrt{x^2+6x+9}\lt 7\\[3pt] &\Leftrightarrow&2(x-1)+(x+3)\lt 7\\[3pt] &\Leftrightarrow&3x\lt 6\\[3pt] &\Leftrightarrow&x\lt 2 \end{eqnarray}$
よって、$1\leqq x\lt 2\quad(\ x\geqq 1\ との共通範囲) $
$\therefore$ (ⅰ),(ⅱ),(ⅲ)より $\boldsymbol{-2\lt x\lt 2}$
裏技的解法
右辺定数型の➀,➁を組み合わせて拡張させることにより、上の例題の(7)~(9)は、以下のような別解(場合分け不要)が可能である。
右辺定数型・改
$\begin{eqnarray} &\ &\textcolor{hotpink}{aの値によらず}\\[5pt] &\ & \begin{cases} \textcolor{cornflowerblue}{|x|=a}&\Leftrightarrow &\textcolor{hotpink}{x=\pm a}\ かつ\ \textcolor{hotpink}{a\geqq 0}\\ \textcolor{cornflowerblue}{|x|\lt a}&\Leftrightarrow &\textcolor{hotpink}{-a\lt x\lt a}\\ \textcolor{cornflowerblue}{|x|\gt a}&\Leftrightarrow &\textcolor{hotpink}{x\lt -a,\ a\lt x}\\ \end{cases} \end{eqnarray}$
≪別解≫
(7)
$\textcolor{hotpink}{|x-3|=2x-5\Leftrightarrow x-3=\pm(2x-5)\ 且つ\ 2x-5\geqq 0}$
よって、
$x=2,\ \dfrac{8}{3}$ 且つ $x\geqq\dfrac{5}{2}$
$\therefore$ $\boldsymbol{x=\dfrac{8}{3}}$
(8)
$\textcolor{hotpink}{|2x-5|\leqq 4-x\Leftrightarrow -4+x\leqq 2x-5\leqq 4-x}$
より、 $1\leqq x$ 且つ $x\leqq 3$
$\therefore$ $\boldsymbol{1\leqq x\leqq 3}$
(9)
$\textcolor{hotpink}{|x-4|\gt 5x\Leftrightarrow x-4\lt -5x,\ 5x\lt x-4}$
より、 $x\lt\dfrac{2}{3}$ 又は $x\lt -1$
$\therefore$ $\boldsymbol{x\lt -1}$


コメント