皆さんは、数学の勉強をするとき、「とりあえず定期の範囲の勉強を!」とか「公式、解法を暗記さえしておけば何とかなるだろう!」と考えていたりしませんか?
確かに、学校の定期テストに向けた勉強は悪いことではないですし、公式や解法を暗記しておくだけで解ける問題も模試などでは一定数存在します。
ですが、こと本番の大学入試となると、それでは突破するのが難しいのが受験数学です。基礎固めが不十分だと、少し応用的な問題になるととたんに太刀打ちできなくなってしまいます。
ここでは、おすすめの参考書や参考書の到達レベル、おすすめの参考書ルートを紹介します。基礎固めから大学入試までの全体像をつかみ、今後の勉強に役立ててください。
参考書選びのポイント
数学の参考書は非常に多くの種類が存在します。そのため、「何を選べばいいの?」と困ってしまうことも多くなります。まずは、参考書を選ぶときに抑えておきたいポイントを3つ紹介します。
参考書ごとの利用目的を確認する
数学に限りませんが、参考書にはそれぞれ種類ごとに「こういう効果を期待する」という使用目的と呼べるものが存在します。自分の目的に合った参考書を選ばないと、学習効率が一気に悪化するので注意してください。
〔網羅系〕
教科書内容がある程度理解できている状態で取り組むべき参考書です。
基本的には例題→解答・解説→類題が含まれるページ構成になっており、分野ごとに基礎→応用と並んでいます。例題とその解説で解法を習得し、類題で定着させるという使い方が基本になります。
網羅系の参考書をしっかりと完成させることで、入試の基礎をがっちりと固めるようにしましょう。
ただし、典型的な解法パターンを広くカバーするために、問題数はかなり多くなってきます。覚悟を持って取り組む必要があります。
〔入試対策系〕
この系統には、基礎固めから大学入試本番を意識したレベルまで幅広い難易度のものが含まれます。
・典型パターンと実際の入試問題の橋渡し
・入試での実戦力強化
・数学で無双するための実力づくり
などが使用目的となります。
〔分野別〕
苦手単元の克服や、志望校に頻出の単元の対策など、強化したい内容が限定されている場合に使用することになります。
〔計算問題集〕
分野別の1つではありますが、あえて分けました。
計算練習は、高校数学では意外と軽視されがちだと感じています。ですが、入試という場においてものをいうのは結局のところ計算力です。特に理系の人はかなりの計算スピードと正確性が要求されます。
計算に少しでも不安がある人はぜひ活用してほしいカテゴリーです。
1冊ずつ完璧に仕上げる意識で進めていく
使用すると決めた参考書は、1冊1冊を確実に仕上げていくことが重要です。(1回で完璧にしろというわけではないので勘違いしないでくださいね。)
中途半端な状態で、いろいろな参考書に手を出してしまうと、「ノウハウコレクター」「参考書マニア」となってしまいがちです。これでは数学力は伸ばせません。本当に注意してください。
基礎固めを軽視しない
参考書学習では、自分のレベルに合っていない参考書を使ってしまうことが起こりがちです。数学が得意だと思っている人であっても、基本的な内容の理解が不十分であるケースが多かったりします。見栄やプライドでレベルの高い参考書に手を出すのではなく、「土台をしっかり固める」ことを意識し、自分のレベルにマッチした参考書を選ぶようにしてください。
また、完全に独学の人だと「志望校の過去問に触れるタイミング」も失敗しやすいので注意が必要です。過去問については”早く触れるべき”という意見と、”早くに触れるべきではない”という意見の両方が存在しています。
私の結論としては、『早めに触れておくべきだが、安易に手を出すべきではない』です。早めに自分の立ち位置を確認し、残りの時間を効率よく使う指針にすることは非常に重要です。が、基礎が固まっていない段階で過去問に触れてもメリットは皆無です。(むしろ心が折られて害にしかなりません。)
本格的に過去問に取り組むのは受験学年の夏前後からというイメージを持ち、あくまでも、「まず基礎を確実に固める。そのうえで、できれば早めに過去問に一度触れておく。」という意識を持つようにしてください。
おすすめの参考書とそのレベル
数多く存在する数学の参考書は、「どのようなレベル帯の人が使うべきなの?」「結局どれを使えばいいの?」と判断に迷うところだと思います。
ここでは、定期テスト対策から、最難関受験者向けまでを、F~SSの8段階で分類して、おすすめの参考書を紹介していきます。
あくまでも私見であることを踏まえて、参考にしてください。
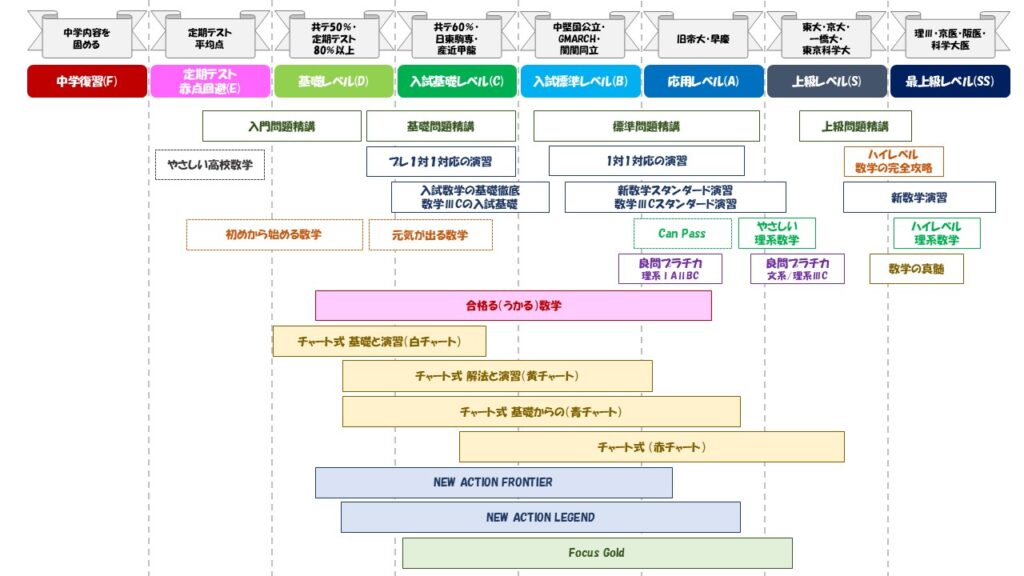
レベルF:中学数学を固めなおすことを目指す。”数学はずっと苦手”という人はここから。
レベルE:定期テスト赤点回避を目指すレベル。教科書内容の整理を確実に行う。
レベルD:高校数学の基礎の完成を目指すレベル。教科書内容を完成させ、共テ5割を目指す。
レベルC:入試基礎レベル。受験数学で必須の基本的な解法(定石)の習得を目指す。
レベルB:入試標準レベル。入試の典型問題に対する対応力を身に着ける。
レベルA:応用レベル。難関大入試の典型問題に対する対応力を身に着ける。
レベルS:上級レベル。東大・京大・一橋大・東京科学大といった最難関大入試に対応できる力を磨く。
レベルSS:最上級レベル。東大理Ⅲ・京医といった、超難関入試で高得点を取る実力鍛える。
入門レベルの参考書
大学受験を意識している人が使う入門レベルの参考書としてオススメなのは
- 入門問題精講
- 初めから始める数学
- 高校これでわかる数学
といった参考書です。
いずれも素晴らしい参考書ですが、私の一押しは『入門問題精講』です。
入試基礎レベルの参考書
入門レベルで教科書レベルの内容を固めた次のステップとして使用するレベルの参考書がこのレベルです。入試レベルと教科書レベルの橋渡しをし、入試の基礎といえる内容をしっかり固める段階になります。
この段階で使用するのにオススメの参考書は
- 基礎問題精講
- 元気が出る数学
- 大学への数学 プレ1対1対応の演習
- 大学への数学 入試数学の基礎徹底
- 大学への数学 数学ⅢCの入試基礎/講義と演習
- 文系の数学 重要事項完全習得編
- 数学Ⅲ 重要事項完全習得編
といった参考書です。
いずれも素晴らしい参考書ですが、特にオススメなのが『プレ1対1対応の演習』と『入試数学の基礎徹底』の併用です。また、『数学ⅢCの入試基礎』も理系の人にはぜひ使ってほしい1冊です。
入試標準~応用レベルの参考書
実際の志望大学合格に向けて必要な学力を伸ばしていく段階で使う参考書たちです。
- 標準問題精講
- 大学への数学 1対1対応の演習
- 大学への数学 新スタンダード演習
- 大学への数学 数学ⅢCスタンダード演習
- 文系の数学 実戦力向上編
- 国公立標準問題集 Can Pass
- 理系数学の良問プラチカ 数学Ⅰ・A・Ⅱ・B・C
- 文系数学入試の核心
- 理系数学入試の核心 標準編
- やさしい理系数学
といった参考書がオススメといえます。
中でもオススメなのが、『1対1対応の演習』と『新数学スタンダード演習』(理系の人はさらに『数学ⅢCスタンダード演習』も)の併用です。正直、好みがわかれる 大学への数学シリーズ ですが、解法に至る思考をすっきりと示してくれる、いい意味で親切でないことがこのレベルの参考書としては非常にポイントが高いと思います。
最難関を目指すのにオススメの参考書
東大・京大・一橋大・東京科学大といった、最難関の大学を目指す場合に取り組みたい参考書・問題集です。
- 文系数学の良問プラチカ 数学Ⅰ・A・Ⅱ・B・C
- 理系数学の良問プラチカ 数学Ⅲ・C
- 上級問題精講
- ハイレベル数学ⅠAⅡBC(ベクトル)の完全攻略
- ハイレベル数学ⅢC(平面上の曲線と複素数平面)の完全攻略
- 大学への数学 新数学演習
- ハイレベル理系数学
- 理系数学入試の核心 難関大編
- 数学の真髄
- 入試数学の掌握
これらはいずれも、実際に過去問を解いてみて必要と感じたら追加するという使い方をお勧めします。あくまでも、過去問を通して志望大学が要求する能力を鍛えることが優先です。
網羅系参考書
網羅系参考書は、基本的には辞書的に扱うイメージでよいでしょう。選ぶ際には、自分が必要とするレベルのものを選ぶことが重要です。
- NEW ACTION FRONTIER
- チャート式 解法と演習(黄チャート)
- 合格る(うかる)数学
などがオススメです。とはいえ、使い方を間違えず、自分のレベルとあっているなら、大きな差は生まれません。学校ですでに購入しているものがある場合、それを使い続けて全く問題ないと考えてください。
※ 学校採用だと、上記のオススメに選んだものよりも、より網羅度が高い(より難しい問題までカバーしているため問題数が多い)、『青チャート』や『Focus Gold』、『NEW ACTION LEGEND』が多い印象です。これらも十分オススメできるので安心してください。
おすすめの参考書ルート
いろいろな参考書がある中で、「実際に何を使うべきか」は結局のところ一人一人違います。とはいえ、「何か参考になる目安が欲しい」というのも理解できます。そこで、これまでの私の経験から「この流れで進めていければ理想的」というおすすめの参考書ルートを紹介したいと思います。
日東駒専/産近甲龍レベル
レベルDでの基礎力完成に注力し、レベルCの問題集で演習することで仕上げていくのが大まかな流れです。
まず、『入門問題精講』で基本原則の理解を進めていきましょう。「なぜその解答になるのか」をきちんと説明し、自力で解答作成できるようになるまで反復してください。
次の段階は、『プレ1対1対応の演習』と『入試数学の基礎徹底』、『数学ⅢCの入試基礎』での徹底的な基礎固めです。『プレ1対1対応の演習』や『数学ⅢCの入試基礎の講義パート』を進めていて少しでも疑問が生じたら入門問題精講に立ち返るようにしてください。
『プレ1対1対応の演習』と『数学ⅢCの入試基礎の講義パート』が仕上がったら、『入試数学の基礎徹底』『数学ⅢCの入試基礎の演習パート』で基礎レベルの問題が解けるように練習していきましょう。
解答を暗記するのではなく、「問題をどのようにとらえて解答すればよいのか」について丁寧に考えることを意識してください。ここまで出来たら、あとは実際の過去問で仕上げていくだけです。
地方国公立大/GMARCH/関関同立レベル
レベルDで基礎を確認した後、レベルCの参考書で入試の基礎を固めていきます。仕上げの演習ではレベルBまでは取り組みたいところです。
まず、『入門問題精講』で基本原則の本質的な理解を進めてください。その後は、『プレ1対1対応の演習』や『入試数学の基礎徹底』、『数学ⅢCの入試基礎』で入試に必要な基本パターンをマスターしていきます。これらが仕上がったら、入試レベルの問題への挑戦です。
●GMARCH/関関同立といった私立大学が志望の人
『1対1対応の演習』の例題に取り組んでください。このときの注意点は、解答を暗記するのではなく、「問題をどのようにとらえて解答すればよいのか」について丁寧に考えることです。文系の人は、『文系の数学』に取り組むのもおすすめです。
● 国公立大学が志望の人
上記に加えて『国公立標準問題集 Can Pass』にも取り組んでください。ここで、国公立大学で出やすい形式の問題に慣れていきます。ここまで進めておけば、金沢大学、広島大学などと同程度のレベルの大学であれば対応できる力が身につきます。
上位国公立大/旧帝大/早慶上理レベル
レベルDで基礎をサクッと確認した後、レベルC~Aの参考書を使って、典型問題に対する解答手法をマスターしていきます。演習に関しては、レベルSに触れておきたいですが、数学にそこまでの時間をかけられない場合にはレベルAまででも構いません。
『入門問題精講』で基本原則の確認をサクッと進めてください。その後は、『プレ1対1対応の演習』や『入試数学の基礎徹底』、『数学ⅢCの入試基礎』で入試に必要な基本パターンをマスターしたうえで、『1対1対応の演習』で解法パターンを増やしていきます。『新数学スタンダード演習』『数学ⅢCスタンダード演習』で演習量を増やし、実力を磨いてください。そのあとは、志望校別に以下に分岐します。
●千葉大学、横浜国立大学、神戸大学、北海道大学、九州大学、上智大、東京理科大学などが志望の人
『Can Pass』の後、『入試の核心(文系/理系 標準編)』を仕上げていきましょう。「時間がない!」という人も『Can Pass』 は確実に仕上げてください。
●東北大学、名古屋大学、大阪大学(医学科除く)、早稲田大学、慶應義塾大学が志望の人
過去問で実際の問題にどの程度対応できるかを確認したうえで、必要であれば『文系数学の良問プラチカ』+『理系数学の良問プラチカⅢC』に取り組んでください。
●東京大学(文科)、京都大学(文系)、一橋大学が志望の人
過去問で実際の問題にどの程度対応できるかを確認したうえで、『ハイレベル数学の完全攻略(通称:ハイ完)』まで進められると理想的です。必要な単元に絞って取り組むのが良いでしょう。
●東京大学(理科)、京都大学(理系)、東京工業大学 東京科学大学、大阪大学(医学科)が志望の人
過去問と並行して『新数学演習』に挑戦してください。このときに、『数学の真髄』『入試数学の掌握』などにも合わせて取り組み、論理的な考察力を強化できると理想的です。
最適な参考書を選択し、数学力を確実に高めよう!
基礎の確実で本質的な理解というのが数学の勉強において最も重要です。実際、最難関大学で出題されるような難易度の高い問題でも、ほとんどの場合「典型問題」の組み合わせになっています。
入試でつまづくのは基礎が固まっていないことがほとんどです。逆に言うと、基礎の本質的な理解ができてしまえば、最難関大学にもつながる地力が身についたということにほかなりません。
丸暗記で目の前のテストを乗り切るというやり方ではなく、一歩一歩地力を高めていく、そんな学習をぜひ進めていってください。





















コメント
理一志望、高2です
とりあえず入門問題精講を3cまで一周したのですが、今後、new action legend やってスタ演をやるのか、入試の基礎徹底、一対一をやってスタ演やるのはどちらがおすすめでしょうか?
コメントありがとうございます。また、返信が遅くなってしまい申し訳ありません。
さて、ご質問の件についてです。
現役での東大合格を考えると、「来年の夏休み以降を、過去問演習中心の学習にできるか」が一つのポイントになります。そしてそのためには、「今年の冬休みからスタ演に取り組める」状況を作らなくてはいけません。
あああ さんのおっしゃる’入門問題精講を3cまで一周した’というのが、「入門精講の中身は完ぺきに仕上がっている状態」ととらえてよいなら、『入試の基礎徹底⇒一対一⇒スタ演』のルートをお勧めします。こちらの方が、より分野として理解を深めて学習していけると思います。
一方で、「入門精講の中身に少しでも不安がある状態」なのであれば『new action legend⇒(一対一)⇒スタ演』のルートをお勧めします。入門精講からのレベルギャップが少なく、無理なくステップアップできるのはこちらです。こちっらのルートの場合も、出来れば一対一はやっておきたいので、「★2以下は飛ばす」など、問題数を圧縮できる工夫をしてもらえるといいかなと思います。
これまでの学習状況や、数学に避ける学習時間などが分からない状況での回答で申し訳ないですが、ぜひ参考にしていただければと思います。
ぜひ、全力で学習に取り組み、現役での合格を勝ち取ってください。