多くの受験生を合格に導いてきた『良問プラチカ』。「聞いたことがある!」「知ってる!」という人もいるのではないでしょうか。また、先輩などから話を聞いて、「難しい」とか「受験生ならみんなやる」というイメージを持っている人も少なくないかもしれません。
そんな本書のタイトルのもとになった”プラチカ(pratica)”はイタリア語で、知識や理論を実際に応用する行為や経験、練習を通して習得することを指すそうです。「実際に問題を解いて練習することで理解を深める」という意図が込められているのがよくわかるタイトルですよね。
この記事では、『良問プラチカ』が”実際どんなレベルなのか”や”使うべき人”、”使うタイミング”などについて詳しくみていきます。 実際に購入する前に、是非この記事の内容を最後まで確認してください。『良問プラチカ』が自分に合うのか、必要なのかをしっかり判断し、最後までやり切る意思を持つ、そのお役にきっと立てるはずです。
なお、プラチカ以外にどんなオススメの参考書があるかを紹介している記事も投稿しています。良ければそちらも参考にしてみてください。
『入試精選問題集 〇〇数学の良問プラチカ』の概要

『良問プラチカ』には 文系 / 理系ⅠAⅡBC / 理系ⅢC の3冊が存在します。
文系、理系と名前がついていることから、
- 難易度:文系 <理系ⅠAⅡBC<理系ⅢC
- 使うべき人:文系プラチカが文系大学志望者 理系プラチカが理系大学志望者
と考えてしまうかもしれません。しかし、実際はこれとは全く異なります。
ここでは、実際のレベルや使ってほしい人について説明していくので、まずは『良問プラチカ』とはいったいどんな参考書なのかを知ってください。
『良問プラチカ』のオススメ度とレベル・問題数・出版社
まずは、文系プラチカ、理系プラチカⅠAⅡBC、理系プラチカⅢCがどのようなレベルで、問題数がどの程度あるのかを紹介します。
詳しくはこの後見ていきますが、3冊のレベルについては理系ⅠAⅡBC≪文系≦理系ⅢC です。決して「文系だから簡単なんでしょ?」のように考えないようにしてくださいね。
文系数学の良問プラチカ 数学ⅠAⅡBC
 〈おすすめ度:★★★☆☆〉
〈おすすめ度:★★★☆☆〉
出版社:河合出版
著 者:鳥山昌純
定 価:1,375円
文系数学といわれると無意識に「理系より簡単」と思いがちですが、そんな気持ちで手を出すと大やけどするのが『文系プラチカ』です。ここでは、そんな『文系プラチカ』について詳しく見ていきます。
文系数学の良問プラチカ 数学ⅠAⅡBCのレベル
先輩や周りで使っている友達などから「難しい」という話を聞いている人もいるかもしれません。それでも、実際に自分で取り組んでみると「こんなに難しいの!?」と感じやすい、そんな問題集です。
●文系プラチカの問題の難易度
東大、京大、一橋大、早慶など最難関とされる大学からの出典が多く、数学ⅠAⅡBCの範囲の問題集としてはほぼ最高難易度といえる1冊です。
文系志望の人にとっては、過去問以外の参考書・問題集としては取り組むべき最後の1冊がこの文系プラチカとなることがほとんどです。
理系志望の場合でも、数学ⅠAⅡBCの範囲の参考書・問題集としては最後に1冊になる可能性が高いです。
『文系プラチカ』と同レベル以上の参考書・問題集を上げると、
新数学スタンダード演習(スタ演) / やさしい理系数学(やさ理) /上級問題精講 / ハイレベル数学〇〇の完全攻略(ハイ完) / ハイレベル理系数学(ハイ理) / 理系数学入試の核心難関大編 / 入試数学の掌握 / 新数学演習(新数演)
といった理系を中心とした最難関大学の入試で高得点を狙う人向けのものばかりです。
●『文系プラチカ』で目指せるレベル
『文系プラチカ』をしっかりと完成させることで、数学ⅠAⅡB(数列)C(ベクトル)の範囲については東大・京大といった最難関大学で合格点を十分狙えるレベルまで到達できます。 ただし、理系志望の人のうち、最難関大学で高得点を取りたい!という場合には、『文系プラチカ』だけではやや不安が残ります。過去問を通じて演習することをメインにしつつ、時間に余裕があれば、先ほど出てきた『文系プラチカ』と同レベル以上の参考書・問題集のうちどれか1つを過去問と並行して進めると安心です。
文系数学の良問プラチカ 数学ⅠAⅡBCの問題数
| 単元 | 問題数 |
|---|---|
| 2次関数、2次方程式、2次不等式 | 10 |
| 図形と計量(三角比) | 5 |
| 図形の性質 | 5 |
| 場合の数、確率 | 21 |
| 整数 | 11 |
| いろいろな式 | 13 |
| 図形と方程式、不等式 | 17 |
| 指数関数、対数関数 | 9 |
| 三角関数 | 9 |
| 微分法、積分法 | 16 |
| 数列 | 20 |
| ベクトル | 23 |
| 合計 | 159 |
『文系プラチカ』に掲載されている問題は、全体として難関大学合格に必要な高いレベルのものになっています。ですが、決してすべての問題が超難問というわけではありません。意外と基本的な問題も含まれていたりします。簡単にはあきらめず、じっくり取り組んでください。
とはいえ、無制限に時間を使って考え込んでしまうのも問題です。何も考えずにすぐ解答をみるのはおすすめできませんが、本番も意識し1問あたり30分程度を目安に、ある程度は時間も意識して取り組むようにしてください。
※数学B・Cは、それぞれ数列・ベクトルのみの収録な点には注意してください。志望校の出題範囲に統計的な推測や二次曲線、複素数平面が含まれるようなら別で演習する必要があります。
理系数学の良問プラチカ 数学ⅠAⅡBC
 〈おすすめ度:★★★☆☆〉
〈おすすめ度:★★★☆☆〉
出版社:河合出版
著 者:大石隆司
定 価:1,375円
文系・理系どちらを志望している人でも効果的に活用できるのが『理系プラチカⅠAⅡBC』です。幅広い人が必要とするレベル感と程よい問題数になっています。そんな『理系プラチカⅠAⅡBC』について詳しく見ていきましょう。
理系数学の良問プラチカ 数学ⅠAⅡBCのレベル
実際に使った多くの受験生が、
「思っていたよりレベルが高いとは感じなかったけど、やってよかったと思える良問ぞろいだった」
という感想をこたえてくれる。そんな問題集が『理系プラチカⅠAⅡBC』です。
●理系プラチカⅠAⅡBCの問題の難易度
多くの受験生がやってよかったと感じる『理系プラチカⅠAⅡBC』に掲載されている問題は、
- 旧帝大の絶対に落としてはいけないレベル
- 地方国公立大学の標準的なレベル
になっています。
『青チャート』や『NEW ACTION LEGEND』のような網羅系参考書や『1対1対応の演習』、『標準問題精講』といった参考書でインプットした知識を、入試標準レベルの良問でアウトプットできる素晴らしい1冊です。 『文系プラチカ』に進む前の基礎力確認にもうってつけといえます。
●『理系プラチカⅠAⅡBC』で目指せるレベル
『理系プラチカⅠAⅡBC』をしっかりと完成させることで、ⅠAⅡBCの範囲については、旧帝大(東大・京大・一橋大・東京科学大などの最難関は除く)や、早慶といった難関大学の入試でなんとかギリギリ合格点をとれる(確実にではない)レベルが到達点です。
最難関大学や難関大学の医学部、早慶の数学で高得点を取る必要があるという人は、『理系プラチカⅠAⅡBC』だけでは確実に不十分です。 『文系プラチカ』や『新数学スタンダード演習(スタ演)』といった最難関大レベルの問題集にステップアップしていきましょう。(東大理Ⅲや京大医学部を目指す人はさらにその先に取り組むことも必要です。)
理系数学の良問プラチカ 数学ⅠAⅡBCの問題数
| 単元 | 問題数 |
|---|---|
| 2次関数 | 8 |
| 数と式 | 16 |
| 図形と計量 | 5 |
| 図形と方程式 | 16 |
| 三角関数 | 12 |
| 指数関数・対数関数 | 10 |
| 微分法 | 9 |
| 積分法 | 11 |
| 場合の数 | 7 |
| 確率 | 11 |
| 数列 | 25 |
| 平面ベクトル | 13 |
| 空間ベクトル | 11 |
| 複素数平面 | 11 |
| 合計 | 165 |
『理系プラチカⅠAⅡBC』に掲載されている問題は、全体として入試標準レベルの典型的な問題で構成されています。取り組む際には、1問あたり20分程度を目安にし、本番の入試に向けたスピードも鍛えていきましょう。
注意点は、分野による問題数の偏りがあることです。自分の志望校の出題傾向を考え、演習量が不足しそうであれば追加で演習量を稼ぐことが必要です。
※数学B・Cに統計的な推測・2次曲線が含まれないことにも注意してください。志望校の出題範囲に含まれるようなら別で演習する必要があります。
理系数学の良問プラチカ 数学ⅢC
 〈おすすめ度:★★★☆☆〉
〈おすすめ度:★★★☆☆〉
出版社:河合出版
著 者:続木勝年 / 宮嶋俊和
定 価:1,320円
同じ『理系数学の良問プラチカ』という名前がついているので同じレベルだと勘違いする人が出てしまうのが『理系プラチカⅢC』です。
プラチカ3冊の中で最高の難易度になっており、「想像以上に難しい」と感じる人が続出する1冊になっています。そんな『理系プラチカⅢC』について詳しく見ていくので、実際に取り組む前にしっかり確認してください。
理系数学の良問プラチカ 数学ⅢCのレベル
実際に自分で取り組んでみると「こんなに難しいの!?」と文系プラチカ以上に感じやすい、のが『理系プラチカⅢC』です。『理系プラチカⅠAⅡBC』に取り組んだ後そのままの感覚で手を出すと大やけどしてしまう問題集なので要注意です。
●理系プラチカⅢCの問題の難易度
『理系プラチカⅢC』に掲載されている問題は、東大・京大・東工大(現:東京科学大)といった最難関大学を中心に、旧帝大や医学部系単科大学などが多くを占めています。
選ばれている問題も、これらの大学に合格する力をみにつけるのに適した難度の高い良問ばかりです。
そのため、多くの受験生にとって、数学ⅢCの範囲の参考書・問題集として取り組む最後に1冊になると思います。
『理系プラチカⅢC』と同レベル以上の参考書・問題集としては、
新数学スタンダード演習(スタ演) / やさしい理系数学(やさ理) /上級問題精講 / ハイレベル数学〇〇の完全攻略(ハイ完) / ハイレベル理系数学(ハイ理) / 理系数学入試の核心難関大編 / 入試数学の掌握 / 新数学演習(新数演)
といった、東大理Ⅲや京大医学部志望の受験生や、難関大で高得点を狙う受験生向けのものがあげられます。
●『理系プラチカⅢC』で目指せるレベル
『理系プラチカⅢC』をきちんと仕上げれば、ほとんどすべての大学の合格レベルに到達可能です。
この1冊だけでは厳しいなと私が判断しているのは
東大理Ⅲ、京大医学科、阪大医学科、東京医科歯科大(現:東京科学大)医学科、慶應義塾大医学科
といった、最難関医学部に限られます。
加えて、これらの大学の医学科であったとしても「数学の得点は合格できるギリギリでもいい」とするなら対応は可能になります。
『理系プラチカⅢC』に掲載されている問題を解けるようになれば、基本的に困る大学はないと考えてもいいレベルに到達できると思ってください。
上記の医学科や、最難関理系学部でも数学を確実な得点源にしたいという人は、過去問を通じて演習することをメインにしつつ、先ほど出てきた『理系プラチカⅢC』と同レベル以上の参考書・問題集の中から状況に合わせてどれか1つに取り組めると安心です。
理系数学の良問プラチカ 数学ⅢCの問題数
| 単元 | 問題数 |
|---|---|
| 極限 | 12 |
| 微分法 | 14 |
| 積分法 | 33 |
| 2次曲線 | 8 |
| 複素数平面 | 9 |
| ベクトル | 4 |
| 合計 | 80 |
『文系プラチカ』や『理系プラチカⅠAⅡBC』と比べて問題数は約半分です。
それでもやりごたえは十分ですが、積分以外の演習量は不足気味です。特に複素数平面の問題数が少ないので要注意です。この問題数で複素数平面のアウトプットが十分という受験生はほぼいないと思います。複素数平面については、追加の演習問題を解くことが必須だと考えておきましょう。
また、『理系プラチカⅢC』に取り組む受験生の多くは『文系プラチカ』にも取り組んでいると思いますが、そうでなければベクトルにも追加の演習が必要です。
良問プラチカの構成
『文系プラチカ』『理系プラチカⅠAⅡBC』『理系プラチカⅢC』いずれも〔問題編(別冊)〕+〔解答編〕の構成になっています。
このレベルの問題集としては解説が詳しいほうで、解答のポイントや別解、背景にある知識の掘り下げなどがなされています。(著者が異なるためレイアウトはそれぞれ異なります。)
とはいえ、ものすごく丁寧な解説という事ではなく、解答や解説の行間をある程度は自分で考えることが必要です。解答や解説をみて、「よくわからない」「もっと丁寧な解説が欲しい」と感じるようであればプラチカに挑戦するのに必要な基礎力が不足している証拠と考え、網羅系参考書などに戻って基礎力を固めなおしましょう。
『プラチカ』に取り組む時期
-1024x576.jpg)
志望校合格に向け、どのタイミングでどの参考書・問題集に取り組むかは非常に重要です。
「やろうとしたけど、本番までに終わらなかった。」とか「何とかやり切ったけど、過去問演習の時間がほとんどとれなかった。」となってしまっては、もともこもありません。
ここでは、『プラチカ』を志望校合格に向けた武器として効果的に活用するのに適した取り組み時期についてみていきます。
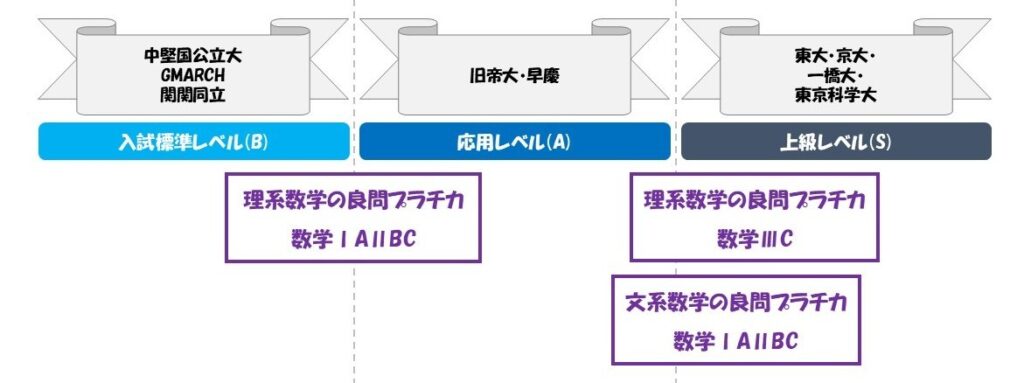
理系数学の良問プラチカ 数学ⅠAⅡBC
中堅国公立大学やGMARCH,関関同立といった大学志望の人
できれば高2の3月、遅くとも高3の4月からは取り組みたいところです。
文系の人は夏休み前までに、理系の人は数学ⅢCの演習(Can Passなど)も含めて夏休み中に一通りやり終えるのが目標になります。
秋以降は、志望校の過去問を中心に学習を進め、必要に応じて入試の核心(文系/理系標準編)などを併用するのがおすすめです。
旧帝大や早慶が志望の人
できれば高2の12月、遅くても高2の1月からは取り組めるように学習を進めていきましょう。
GW明けから過去問演習に着手できるように進めてください。
夏以降は、数学の目標得点をどのくらいと考えるかどうかでやるべきことが変わります。ある程度の得点を目指したい人は文系プラチカ、理系プラチカⅢCを、そうでない人は入試の核心(文系/理系標準編)を進めるのがオススメです。
文系数学の良問プラチカ 数学ⅠAⅡBC / 理系数学の良問プラチカ 数学ⅢC
旧帝大や早慶が志望の人
無理をして取り組む必要はありません。数学である程度の点数を見込んでおきたい!という人のみ使用するものと考えましょう。
取り組むタイミングは、高3の秋以降です。夏の間に一旦過去問演習を行い、自分に必要な分野に絞って取り組むようにしましょう。
数学はそこそこの得点でいいと考える人は、入試の核心(文系/理系標準編)などで、入試標準レベルをより確実に解けるようにすることが重要です。
いずれにしても、高3の夏以降のメインは過去問を使っての学習を進めてください。
東大(理Ⅲ除く)、京大(医学科除く)、一橋大、東京科学大(医学科除く)が志望の人
高3のGW明けにはプラチカを終えることが目標になります。そのため、高2の1月には着手できるようにしてください。
数学に苦手意識がある場合は、理系プラチカⅠAⅡBCに一旦取り組むのも効果的です。この場合、理系プラチカⅠAⅡBCに取り組み始めるのは遅くとも高2の12月となります。
夏休みの間に過去問に取り組み、秋以降は過去問と並行して頻出分野から順にプラチカレベルを固めてください。
東大理Ⅲ、京大医学科、阪大医学科、東京科学大医学科などが志望の人
文系プラチカと理系プラチカⅢCの両方を高2の3月には終えるのが目標になります。そのため、開始時期としては遅くとも高2の12月です。
その後は、GW有効に活用し、春の間に5年分以上を目安に一旦過去問を解きましょう。
夏以降は、過去問演習と並行して『新数演』『ハイ完』などで頻出分野から順に磨きをかけていきましょう。
『プラチカ』の効果的な使い方
参考書・問題集は取り組み方によってもその効果が大きく変わります。せっかく取り組んでも、やり方がまずいとほとんど効果が得られず時間の浪費をしただけという事になりかねません。そのような悲惨な事態を招かないように、おすすめの使い方を紹介します。
1周目の流れ
1周目のポイントは解法をじっくり考えることです。網羅系や問題精講シリーズと異なり、これまでに学習してきた内容を実際に使えるようにトレーニングするのが目的だからです。これまでにインプットで使用してきた参考書を確認しながらでも構わないので、自力で解答を作ってみるようにしましょう。
- 問題を解く
まずは、問題が解けるかチャレンジしましょう。
すぐに解答をみるのではなく、『理系プラチカⅠAⅡBC』であれば20分を、『文系プラチカ』『理系プラチカⅢC』であれば30分を目安にじっくり考えるようにしてください。
このとき、「人に聞く」「解答をみる」以外の方法でいろいろと調べながら解答を作るのはありだと思ってください。
ともかく自分の頭と手を動かして答案を作るようにしましょう。 - 解法を確認する
答案が作れたら、解答を確認してください。
このとき大切なのは問題をどのようにとらえ、どのような発想をすればよかったかを考えることです。
たんに解答を見て覚えるだけでは本番に生かせる実力は磨けません。
1周目では解ける問題のほうが少ないかもしれません。ですが、これは誰でも(東大合格者であっても)同じなので、気にする必要はありません。これまでに手に入れてきた武器(典型問題の解法パターンなど)の使い方を知るために演習しているのですから、初めは解けなくて当然という気持ちでいましょう。
プラチカの問題は簡単に解けるようなものではありません。本番に向けて時間を意識することは大切ですが、1周目では時間よりも「考え抜く」ほうが優先度は高いことを覚えておいてください。
とはいえ、1問に1時間かけるなどになると非効率ですので、引き際の判断も大切です。
2周目以降の流れ
2周目以降の目的は、実践で生きる解答力を磨き上げることです。問題に正面から向き合うことに加え、時間にもしっかりと意識を向けて取り組んでください。
- 前回の周回のときに解けなかった問題を中心に取り組む
1周目のときと同様に、問題を解いていきますが、できる限り調べないで自力で考えきることが重要です。
いつまでも調べればいいやという気持ちでは、自分で考える力(発想力)は獲得できません。
また、タイマーなどで時間を計り、時間をしっかり意識して解くことも重要です。
なお、〇のついている問題はサッと確認するだけ(頭の中で解答を再現する)でも構いません。3周目以降は〇が2つついているものは完全にスキップしてしまうのもありです。 - 志望校の入試問題で実際に使えるかを確認する
7~8割の問題に解答できるようになったら、実際に共通テストや自分の志望校の過去問に挑戦してみましょう。
実際の入試問題でどの程度通用するのかを確認することで、自分に必要なことが見えてきます。
「この問題を解いたとき何を考えてたっけ?」となってからの復習では効果は薄くなってしまいます。自分なりの攻略法の記憶が鮮明なうちに、どこを修正する必要があったのかを確認するようにしましょう。
『プラチカ』の後にやるべきこと
『プラチカ』を終えた後は実際に過去問を解くようにしてください。
共通テストや志望校の形式や頻出分野を知り、それに合わせて自分の能力を磨き上げていくには、少なくとも過去問10年分は必要です。
10年分の過去問を、本番と同じように時間を測り、きっちりと解きなおしまで行います。また、できた問題についてもより効率的な別解がないかを考えることが必要です。
当然、これらをきっちりと実行しようとすると、相当な時間と労力が必要になります。そのため、の時間を十分確保できるように、『プラチカ』を終えたらまずは過去問に着手しましょう。
そして、過去問を徹底的にやりこむ中で、「この部分が弱い」「ここを鍛えればもっと強みにできる」という自分に必要なことがはっきりし、時間的な余裕が残されている場合にのみ、ほかの参考書・問題集に取り組むようにしましょう。
志望校合格へ向けた『プラチカ』活用のポイント
今回は『文系プラチカ』『理系プラチカⅠAⅡBC』『理系プラチカⅢC』について、難易度や使い方をご紹介してきました。最後に、プラチカを最大限に活用するためのポイントをまとめておきます。
まず、プラチカに取り組むには、基礎が十分に固まっていることが前提です。『NEW ACTION LEGEND』や『青チャート』などで基礎をしっかりと固めてから取り組むべき問題集だという事は忘れないようにしてください。
また、プラチカに取り組む際には「いつまでに」を明確にしておくことも重要です。受験本番から逆算して、計画的に取り組むようにしましょう。
実際に取り組む際には、じっくり考えて答案を作ることが大切です。2周目以降は時間もしっかり意識し、スピードと正確性を高めることも目指してください。
プラチカを終えたら、志望校の過去問に取り組み、実力の仕上げを行います。過去問を通じて、志望校の出題傾向や頻出分野に慣れ、プラチカでみにつけた「自分で考える力(発想力)」を実際の試験問題でより洗練されたものにしていきましょう。
加えて、超難関大学を目指す場合は、『新数学演習(新数演)』や『ハイレベル数学〇〇の完全攻略(ハイ完)』でプラチカ以上にレベルの高い問題にも取り組み、応用力・発想力をさらに鍛えることも有効です。必要に応じてうまく併用してください。
『良問プラチカ』は非常に素晴らしい問題集です。ぜひ最大限に活用し、志望校合格に必要な実力を磨き上げてください!





コメント