ここでは、放物線の2本の接線が直交する場合の交点の軌跡についてみていく。初めに結果を示しておくと、この軌跡は直線となり、準線と呼ばれる。詳しくは、数学Cにて学習するので、そちらを確認してみてほしい。
放物線の準線
放物線 $y=\dfrac{1}{4p}x^2$ において、その直交する2本の接線の交点は
直線 $y=-p$
となり、放物線 $y=\dfrac{1}{4p}x^2$ の準線と呼ぶ。
理系の人は数学Cで改めて学習するので、今は「そんな呼び方するんだ~」と記憶の端にとどめておいてほしい。では、早速だが以下の例題にチャレンジしてみほしい。
例題に挑戦しよう
≪問題≫
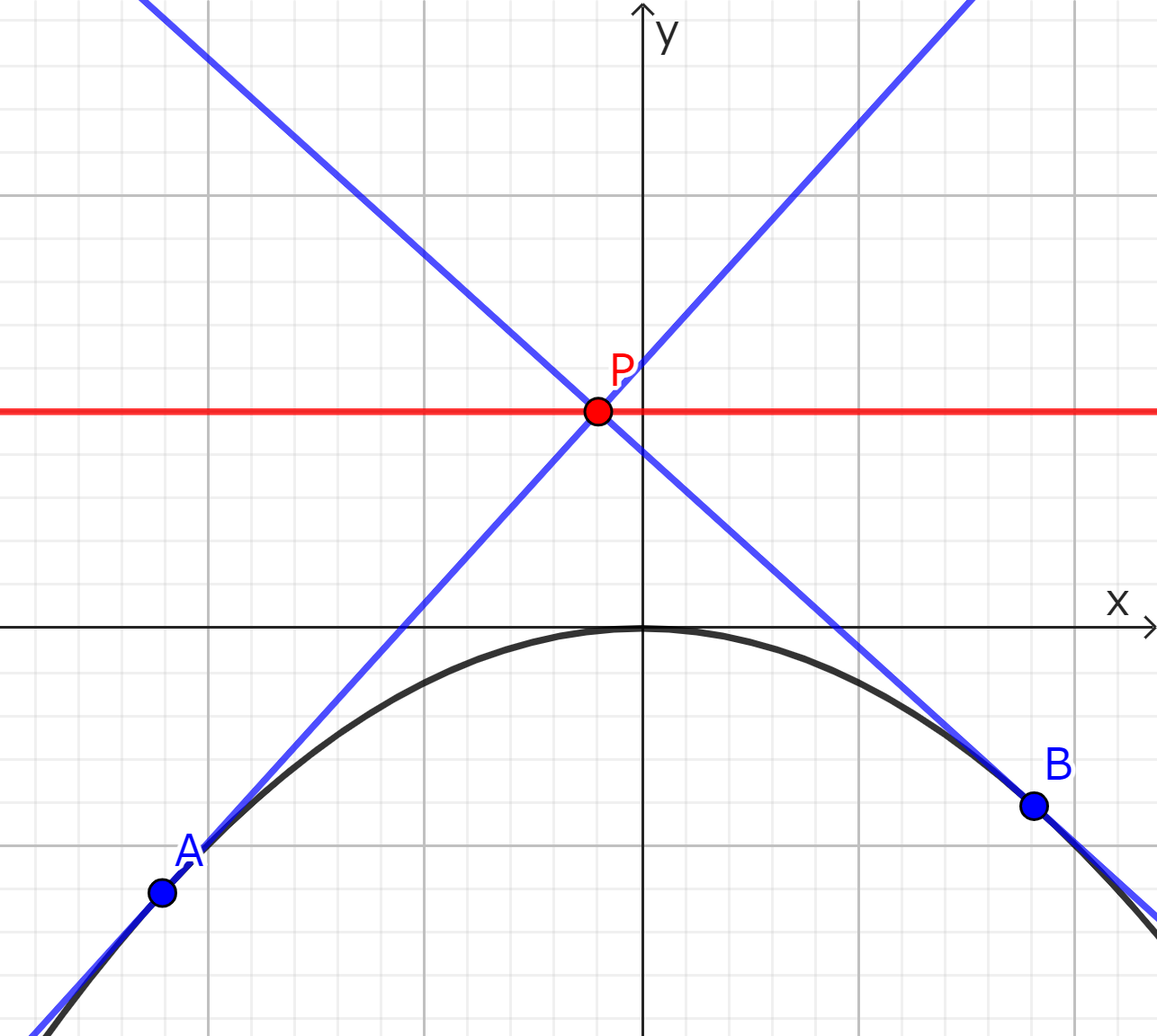
放物線 $y=-\dfrac{1}{2}x^2$ 上の異なる2点$A$,$B$における2本の接線が直交するとき、2本の接線の交点の軌跡を求めよ。
≪解答・解説≫
※接点が不明なので、2つの接点を文字で置き、接線の方程式を求める。
※2直線$y=m_1x+n_1$と$y=m_2x+n_2$が直交する条件は$\boldsymbol{m_1m_2=-1}$
※一般に、$y=ax^2$ 上の2点、$A(α,aα^2)$, $B(β,aβ^2)$における接線の交点は、$\boldsymbol{(\dfrac{α+β}{2},aαβ)}$であらわされる。
$A(α,α^2)$, $B(β,β^2)$ とする。
$y=-\dfrac{1}{2}x^2$ より、
点$A$における接線の方程式は $y=-αx+\dfrac{1}{2}α^2$
点$B$における接線の方程式は $y=-βx+\dfrac{1}{2}β^2$
この2本の接線が直交することから、 $(-α)(-β)=-1 \Leftrightarrow αβ=-1$ である。
また、➀と➁の交点の座標は、 $(x,y)=(\dfrac{α+β}{2},-\dfrac{1}{2}αβ)$ となるので、
2本の接線の交点を$(X,Y)$ とすると、 $(X,Y)=(\dfrac{α+β}{2},\dfrac{1}{2})$ となる。
ここで、$α,β$ は$t^2-(α+β)t+αβ=0$ の異なる2解であるから、その判別式$(D)$は
$D=(α+β)^2-4αβ=(2X)^2-4(-1)=4X^2+4>0$
よって、すべての実数$X$について$D>0$である。
∴求める軌跡は、直線 $\boldsymbol{y=\dfrac{1}{2}}$
※2接線の交点が$(\dfrac{α+β}{2},aαβ)$ で示されるという結果は意外とよく出てくる。理系の人は特に、見通しをよくするためにも覚えておくのがよい。特に、$x$座標が$a$の値によらず常に$\dfrac{α+β}{2}$となることつまり、$\boldsymbol{常にαとβの中央になる}$という性質を抑えておくのは重要である。
【別解】
※軌跡の問題の基本に従い、動点を$(X,Y)$と置いて解き進める。
※$x$軸と垂直な場合の検討を忘れずに行う必要がある。
※微分を使わない方法なので、未学習でもこの方法なら解答できる!
軌跡上の動点を$(X,Y)$ とする。
$y=-\dfrac{1}{2}x^2$の接線が$x$軸に垂直になることはないので、点$(X,Y)$を通り、傾き$m$の直線の方程式は
$y=m(x-X)+Y$
これと、$y=-\dfrac{1}{2}x^2$を連立すると、
$\dfrac{1}{2}x^2+mx-mX+Y=0 \cdots ➀$
$y=m(x-X)+Y$と$y=-\dfrac{1}{2}x^2$が接する条件は➀の判別式$(D_1)$について
$D_1=m^2+2mX-2Y=0 \cdots ➁$
であり、➁が2つの異なる実数解を持つ条件は➁の判別式$(D_2)$について、
$\dfrac{D_2}{4}=X^2+2Y>0 \Leftrightarrow X^2>-2Y \cdots ➂$
この時、➁の異なる2つの実数解を$m_1,m_2$とすると、解と係数の関係より $m_1m_2=-2Y$ であり、2本の接線が直交することから、 $m_1m_2=-1$ であるから、 $Y=\dfrac{1}{2}$
このとき、➂はすべての実数$X$について成り立つ。
∴求める軌跡は、直線 $\boldsymbol{y=\dfrac{1}{2}}$


コメント