因数分解

2次式の因数分解の公式は、じっしつ中学校範囲ですべて学習済みである。忘れているものがある人は、確実にすべて復習してほしい。実際の問題では、『公式の形であることに気付けるか』が勝負になる。

因数分解の公式とたすき掛け

因数分解の公式

$\begin{eqnarray} &[1]& \quad ma+mb=m(a+b)\\[5pt] &[2]& \quad\left\{ \begin{array}{1} a^2+2ab+b^2=(a+b)^2\\ a^2-2ab+b^2=(a-b)^2 \end{array} \right.\\[5pt] &[3]&\quad a^2-b^2=(a+b)(a-b)\\[5pt] &[4]&\quad x^2+(a+b)x+ab=(x+a)(x+b)\\[15pt] &[5]&\quad \textcolor{hotpink}{acx^2+(ad+bc)xy+bdy^2}=\textcolor{cornflowerblue}{(ax+by)(cx+dy)}\\[15pt] &[6]& \quad\left\{ \begin{array}{1} \textcolor{hotpink}{a^3+3a^2b+3ab^2+b^3}=\textcolor{cornflowerblue}{(a+b)^3}\\ \textcolor{hotpink}{a^3-3a^2b+3ab^2-b^3}=\textcolor{cornflowerblue}{(a-b)^3} \end{array} \right.\\[5pt] &[7]& \quad\left\{ \begin{array}{1} \textcolor{hotpink}{a^3+b^3}=\textcolor{cornflowerblue}{(a+b)(a^2-ab+b^2)}\\ \textcolor{hotpink}{a^3-b^3}=\textcolor{cornflowerblue}{(a-b)(a^2+ab+b^2)} \end{array} \right.\\[10pt] &[8]&\quad n=”奇数”\ のとき\\ & \quad & \quad\textcolor{hotpink}{a^n+b^n}=\textcolor{cornflowerblue}{(a+b)(a^{n-1}-a^{n-2}b+\cdots -ab^{n-2}+b^{n-1})}\\ &\quad &\quad n=”整数”\ のとき\\ & \quad & \quad\textcolor{hotpink}{a^n-b^n}=\textcolor{cornflowerblue}{(a-b)(a^{n-1}+a^{n-2}b\cdots +ab^{n-2}+b^{n-1})}\\[10pt] &[9]&\quad\textcolor{hotpink}{a^2+b^2+c^2+2ab+2bc+2ca}=\textcolor{cornflowerblue}{(a+b+c)^2}\\[5pt] &[10]&\quad\textcolor{hotpink}{a^3+b^3+c^3-3abc}=\textcolor{cornflowerblue}{(a+b+c)(a^2+b^2+c^2-ab-bc-ca)} \end{eqnarray}$

※[1]～[4]は中学で学習している。忘れているもんがあれば必ず頭に入れておかなければならない。
※[5]は[4]を一般化したもの。暗記するものではなく、たすき掛けにより因数分解する。
※[6]以降は教科書の発展(又は数Ⅱ,B)や場合によっては扱われていないこともあるが、すべて入試には必須である。ぜひ、ここで押さえてしまってほしい。
※[8]は[7]を一般化したものである。暗算できるものも増え、計算時間だけでなく計算ミスも減らせるはずである。

たすき掛け

公式[5]のような、2次3項式は”展開は容易であるが因数分解は難しい”ものである。ここでは、どのように考え因数分解を進めるかを確認していく。

$2x^2+5xy+3y^2$を因数分解してみよう。
公式[5]の左辺は$\textcolor{cornflowerblue}{ac}x^2+(\textcolor{palevioletred}{ad+bc})xy+\textcolor{limegreen}{bd}y^2$であったから、これらを見比べてみると
$\textcolor{cornflowerblue}{ac=2}$, $\textcolor{palevioletred}{ad+bc=5}$, $\textcolor{limegreen}{bd=3}$　 である。これらを満たすような、整数 $a,\ b,\ c,\ d$ を求めることができれば公式の右辺のように$(ax+by)(cx+dy)$と因数分解できる。

この$a,\ b,\ c,\ d$ を求めるとき、わかりやすく表にまとめて考えることが一般的であり、この作業をたすき掛けという。

たすき掛けの手順
<1>　枠を作り、$\textcolor{cornflowerblue}{2(x^2の係数)}$, $\textcolor{limegreen}{3(y^2の係数)}$, $\textcolor{palevioletred}{5(xyの係数)}$ を下に書く。

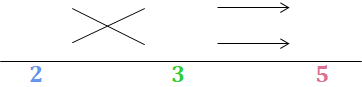
<2>　掛けて2となる自然数の組み合わせを考え、$\textcolor{cornflowerblue}{2}$ の上に書く。

<3>　掛けて3となる整数の組み合わせを考え、$\textcolor{limegreen}{3}$ の上に書く。
※今回の場合だと、$1\times 3$, $3\times 1$, $(-1)\times (-3)$, $(-3) \times (-1)$ の4組が候補である。

<4>　斜めに掛け合わせた答えを矢印の右に書き、それらの和が$\textcolor{palevioletred}{5}$ となるかを確認する。（ならなければ<3>に戻り別の組合せにして考える。）

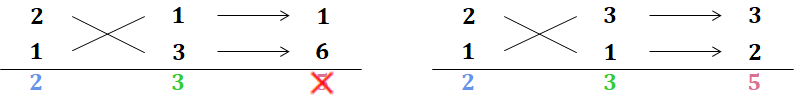
<5>　下図で、左右を見比べると$\textcolor{hotpink}{a=2}$, $\textcolor{hotpink}{b=3}$, $\textcolor{hotpink}{c=1}$, $\textcolor{hotpink}{d=1}$ であることがわかる。

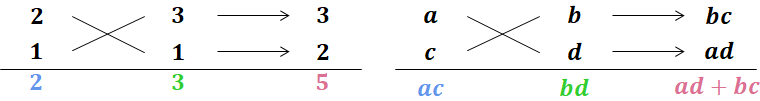
以上により、$2x^2+5xy+3y^2=\boldsymbol{(x+1)(2x+3)}$ と因数分解できる。


※今回の例では $x^2$ の係数が $2$ であるため、検討するのは<3>の4組だけで済む。
しかし、例えば $x^2$ の係数が $16$ ならば<2>の時点で候補となる組み合わせが $1\times 16$, $2\times 8$, $4\times 4$ の3パターン考えられる。このような場合、まず $1\times 16$ で<3>の4組について確認し、ダメなら $2\times 8$ で<3>の4組について確認し…と続けていくことになる。

このように、各項の係数の約数が多くなるに従い、考えなくてはいけない組み合わせが大幅に増えていく。
とにかくたくさん演習し、組み合わせを見つけるまでの思考を洗練させて、感や閃きに頼ることなく素早く $a$, $b$, $c$, $d$ を特定できるようになってほしい。

因数分解の流れ

ここまで、覚えておくべき公式を確認してきた。ここからは、実際に問題を解く手順について確認していく。

因数分解の問題は、解くための手順が（工夫）が存在する。複雑そうに見えるものであっても、手順通りに進めるだけなのである。決して感や閃きに頼るようなものではないことを肝に銘じてほしい。

因数分解を進める手順

[Ⅰ]　共通因数があれば必ず括りだす。
※これを行わずに先に進んでしまうと高い確率で失敗する。
[Ⅱ]　公式に当てはまるか確認する。
※ここまでで解けてしまうものも意外と存在する。
[Ⅲ]　同じ形になっているところを置き換えて公式に当てはまるか確認する。
[Ⅳ]　複数(2種類以上)の文字を含む場合、最低次数の文字に注目して整理する。
[Ⅴ]　複2次式になっているか確認する。
※複2次式である場合、強引に式変形できる。

以下の例題で、実際に確認してほしい。

例題に挑戦しよう

≪問題≫

次の式を因数分解せよ。
(1)　$12xy^3-27x^3y$
(2)　$6x^2+10xy+4y^2$
(3)　$3x^3+6y^3+2x^2y+9xy^2$
(4)　$27x^3+54x^2y+36xy^2+8y^3$
(5)　$2x^2-3y^2-5xy+11y+x-6$
(6)　$4x^4-14x^2y^2+y^4$
(7)　$x^3-8y^3-27z^3-18xyz$
(8)　$(x-9)(x-7)(x-5)(x-3)+15$

≪解答・解説≫

(1) ※手順[Ⅰ]→[Ⅱ]と進み、公式[3]に当てはめる。
$\begin{eqnarray} &\quad &12xy^3-27x^3y\\[5pt] &=&3xy(4y^2-9x^2)\\[5pt] &=&\boldsymbol{3xy(2y-3x)(2y+3x)} \end{eqnarray}$

(2) ※手順[Ⅰ]→[Ⅱ]と進み、公式[5]に当てはめる(たすき掛けする)。
$\begin{eqnarray} &\quad &6x^2+10xy+4y^2\\[5pt] &=&2(3x^2+5xy+2y^2)\\[5pt] &=&\boldsymbol{2(x+y)(3x+2y)} \end{eqnarray}$

(3) ※与えられた式を2行目のように並べ替えた後、手順[Ⅰ]→[Ⅲ]と進み、公式[1]に当てはめる。
$\begin{eqnarray} &\quad &3x^3+6y^3+2x^2y+9xy^2\\[5pt] &=&3x^3+9xy^2+2x^2y+6y^3\\[5pt] &=&3x\textcolor{palevioletred}{(x^2+3y^2)}+2y\textcolor{palevioletred}{(x^2+3y^2)}\\[5pt] &=&\boldsymbol{(3x+2y)(x^2+3y^2)} \end{eqnarray}$

【別解】
$\begin{eqnarray} &\quad &3x^3+6y^3+2x^2y+9xy^2\\[5pt] &=&3x^3+2x^2y+9xy^2+6y^3\\[5pt] &=&x^2\textcolor{cornflowerblue}{(3x+2y)}+3y^2\textcolor{cornflowerblue}{(3x+2y)}\\[5pt] &=&\boldsymbol{(3x+2y)(x^2+3y^2)} \end{eqnarray}$

(4) ※手順[Ⅱ]で、公式[6]に当てはめる。公式の形に気付けるかが勝負のpoint!である。
$\begin{eqnarray} &\quad &27x^3+54x^2y+36xy^2+8y^3\\[5pt] &=&\textcolor{palevioletred}{(3x)^3+3(3x)^2(2y)+3(3x)(2y)^2+(2y)^3}\\[5pt] &=&\boldsymbol{(3x+2y)^3} \end{eqnarray}$

【別解】※公式[6]を覚えていなかった場合、以下のように非常に遠回りである。公式[7]も覚えれていなかった場合には、最終手段の因数定理(数Ⅱ)を持ち出す必要がある。
$\begin{eqnarray} &\quad &27x^3+54x^2y+36xy^2+8y^3\\[5pt] &=&\textcolor{cornflowerblue}{27x^3+8y^3}+\textcolor{limegreen}{54x^2y+36xy^2}\\[5pt] &=&\textcolor{cornflowerblue}{(3x+2y)(9x^2-6xy+4y^2)}+\textcolor{limegreen}{18xy(3x+2y)}\\[5pt] &=&\textcolor{palevioletred}{(3x+2y)}(9x^2-6xy+18xy+4y^2)\\[5pt] &=&\boldsymbol{(3x+2y)^3} \end{eqnarray}$

(5) ※共通因数もなく、このまま公式にも当てはまらない。さらに、同じ形になっている部分も見えてこない。よって、手順[Ⅳ]へと進む。
$\begin{eqnarray} &\quad &2x^2-3y^2-5xy+11y+x-6\\[5pt] &=&2x^2+(1-5y)x-\textcolor{palevioletred}{(3y^2-11y+6)}\\[5pt] &=&2x^2+(1-5y)x-\textcolor{palevioletred}{(3y-2)(y-3)}\\[5pt] &=&\{x-\textcolor{palevioletred}{(3y-2)}\}\{2x+\textcolor{palevioletred}{(y-3)}\}\\[5pt] &=&\boldsymbol{(x-3y+2)(2x+y-3)} \end{eqnarray}$

(6) ※共通因数もなく、このまま公式にも当てはまらない。さらに、$x^2=A$, $y^2=B$ と置くことができそうであるが、うまく公式に当てはまらない。よって、手順[Ⅴ]へと進む。
$\begin{eqnarray} &\quad &4x^4-14x^2y^2+y^4\\[5pt] &=&\textcolor{palevioletred}{(4x^4+y^4)}-14x^2y^2\\[5pt] &=&\textcolor{palevioletred}{(2x^2+y^2)^2-2x^2y^2}-14x^2y^2\\[5pt] &=&(2x^2+y^2)^2-16x^2y^2\\[5pt] &=&\textcolor{cornflowerblue}{(2x^2+y^2)^2-(4xy)^2}\\[5pt] &=&\textcolor{cornflowerblue}{\{(2x^2+y^2)+4xy\}\{(2x^2+y^2)-4xy\}}\\[5pt] &=&\boldsymbol{(2x^2+4xy+y^2)(2x^2-4xy+y^2)} \end{eqnarray}$

※このように、複2次式(2乗の2次式)になっている場合、置き換えてのたすき掛けがうまくいかない場合にも、強引に $A^2-B^2$ の形が作れる場合がある。(これが無理なら因数分解できないのであきらめる。)

(7) ※手順[Ⅱ]で、公式[10]に当てはめる。公式の形に気付けるかが勝負のpoint!である。
$\begin{eqnarray} &\quad &x^3-8y^3-27z^3-18xyz\\[5pt] &=&x^3+(-2y)^3+(-3z)^3-3x(-2y)(-3z)\\[5pt] &=&\boldsymbol{(x-2y-3z)(x^2+4y^2+9z^2+2xy-6yz+3zx)} \end{eqnarray}$

【別解】 ※この公式は導出過程も非常に重要である。是非、別解のルートでも解いてみてほしい。
$\begin{eqnarray} &\quad &\textcolor{palevioletred}{x^3-8y^3}-27z^3-18xyz\\[5pt] &=&\textcolor{palevioletred}{(x-2y)^3-6xy(x-2y)}-27z^3-18xyz\\[5pt] &=&\textcolor{cornflowerblue}{(x-2y)^3-27z^3}+6xy(x-2y)-18xyz\\[5pt] &=&\textcolor{cornflowerblue}{\{(x-2y)-3z\}\{(x-2y)^2+3(x-2y)z+9z^2\}}+6xy(x-2y-3z)\\[5pt] &=&\textcolor{limegreen}{(x-2y-3z)}(x^2+4y^2+9z^2-4xy-6yz+3zx)+6xy\textcolor{limegreen}{(x-2y-3z)}\\[5pt] &=&\boldsymbol{(x-2y-3z)(x^2+4y^2+9z^2+2xy-6yz+3zx)} \end{eqnarray}$

(8) ※いったん展開することで、手順[Ⅲ]に持ち込める。
$\begin{eqnarray} &\quad &(x-9)(x-7)(x-5)(x-3)+15\\[5pt] &=&(x-9)(x-3)(x-7)(x-5)+15\\[5pt] &=&\{\textcolor{cornflowerblue}{(x^2-12x)}+27\}\{\textcolor{cornflowerblue}{(x^2-12x)}+35\}+15\\[5pt] &=&\textcolor{cornflowerblue}{(x^2-12x)}^2+62\textcolor{cornflowerblue}{(x^2-12x)}+960\\[5pt] &=&\{\textcolor{cornflowerblue}{(x^2-12x)}+32\}\{\textcolor{cornflowerblue}{(x^2-12x)}+30\}\\[5pt] &=&\boldsymbol{(x-4)(x-8)(x^2-12x+30)} \end{eqnarray}$