和の法則と積の法則

場合の数の問題を解くうえでもっとも基本になる原則は、中学で学んだ「樹形図」「辞書式配列」「表」などを用いて、『もれなく』『重複なく』すべてを書き出すことである。

とはいえ、試験時間が有限である以上、場合の数が多くなればなるほどすべて書き出すことは現実的でなくなる。そこで重要となるのが「和の法則」と「積の法則」である。

[1]　和の法則

2つの事柄$\ A,\ B \ $において、$A\ $が$\ m\ $通り、$B\ $が$\ n\ $通り考えられるとする。
$A,\ B\ $が同時に起こることがないとすると、
$A\ $または$\ B\ $の起こる場合の数は$\quad m+n\ $通りである。

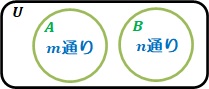
これは、上のベン図を考えると当然のことを言っているだけであり、
●共通部分が存在しない$\ (\ \textcolor{limegreen}{n(A \cap B)=\varnothing} \ ,\ \textcolor{limegreen}{AとBが互いに排反である})\ $ならば、$n(A \cup B)=n(A)+n(B)$
●共通部分が存在する$\ (\ \textcolor{limegreen}{n(A \cap B)\neq \varnothing} \ ,\ \textcolor{limegreen}{AとBが互いに排反でない})\ $ならば、$n(A \cup B)=n(A)+n(B)-n(A\cap B)$
として求めることになる。

これは、場合の数を考える際に「可能な限り排反になる（和の法則を使える）ように場合を分ける」ことが非常に大切であることを示している。排反になるように分けなかった場合、後で共通部分を引くという作業が必要となり、非常に煩雑になることが多いため、間違える可能性が極めて高くなるので強く意識したいポイントである。

[2]　積の法則

2つの事柄$\ A,\ B \ $において、$A\ $が$\ m\ $通り起こり、そのおのおのの場合について、$B\ $が$\ n\ $通り考えられるとすると、
$A\ $と$\ B\ $が同時に起きる場合の数は$\quad mn\ $通りである。

こちらは、樹形図を基に考えるとその理解がしやすい。樹形図で問題を解く際、途中で明確なパターンがあることに気付くことが多い。そして、パターンがあるのであれば、わざわざすべてを書き出さずとも計算で求めれば楽である。

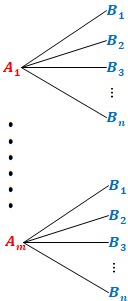
この計算方法の規則が「積の法則」であり、$\ m\ $通りのすべてに対して$\ n\ $通りの可能性があるなら、$m\times n\ $通りとして求めることができる。