皆さんは、『大学への数学 1対1対応の演習(略称:1対1)』シリーズをご存じですか?中堅以上の理系大学志望者や難関大志望者に人気のシリーズなので、知っているという人も多いかもしれませんね。とはいえ、「実際どれくらいのレベルなのか」や、「効果的な使い方」まで詳しく知っているという人はそこまで多くないのではないでしょうか。
『1対1対応の演習』は、多くの受験生に愛されてきた非常に素晴らしい参考書です。入試標準~応用レベルの厳選された問題と丁寧な解説により、独学でもスムーズに学習を進められるようになっています。『大学への数学(略称:大数)』シリーズの中では基本的な問題を扱っているという立ち位置の『1対1』ですが、難関大学合格に向けた実力を本当の意味で固めることができる1冊だと思ってください。
この記事を通して『大学への数学 1対1対応の演習』の特徴や活用法をしっかり理解し、志望校合格に向けて効率よく学習を進めてください。
なお、シリーズ全体の比較や、もっと幅広くおすすめ参考書を紹介している記事も投稿しています。まだ読んでいないという人は、是非そちらも参考にしてみてください。
『1対1対応の演習』の概要
出版社とおすすめ度

〈おすすめ度:★★★★★〉
出版社:東京出版
サイズ:B5判
『1対1対応の演習』は、入試標準~応用レベルの問題に対応できる力を得るための参考書です。
1冊1冊は薄く、問題数も多くはありません。ですが、数学Ⅰ/数学A/数学Ⅱ/数学B/数学Ⅲ/数学C と、文系で4冊、理系で6冊必要になります。学習計画をきちんと立てていないと「終わり切らない…」となるので注意が必要です。
『1対1対応の演習』の構成
〔要点の整理〕〔例題〕〔前文〕〔解答解説〕〔演習題〕〔(超)ミニ講座〕〔コラム〕の7つのパートで構成されています。
- 要点の整理
それぞれの分野ごとに、必要な定義や公式、用語などをすっきりコンパクトにまとめています。教科書と入試レベルのギャップを埋めるための必須事項もまとめられているのがうれしいポイントです。 - 例題
入試標準レベルの問題の中から、典型的かつ汎用性の高い必須問題と、合否への影響が大きい問題という点から厳選された問題が掲載されています。例題レベルをきっちり仕上げることで、中堅国公立大学やGMARCH・関関同立といった大学の入試問題に対応できる実力は身につきます。 - 前文
そのテーマを習得するうえで重要になる手法や思考プロセスがまとめられています。スッキリとした記載のため一見不親切に見えますが、実際はかなり丁寧な内容になっています。 - 解答解説
実際の答案として再現する価値の高い「自然ですっきりとした」解答が記載されています。行間を埋めるために必要な傍注(補足説明)も丁寧で、重要なポイントの理解を深めることが容易になっています。 - 演習題
例題のテーマと1対1に対応した同じテーマの類題です。チャートなどにみられる「単純に同じやり方を再現すれば解ける」というパターンではなく、「例題で学んだ解法をきちんと運用できれば解ける」タイプの問題になっています。
そのため、例題よりも1ランク難易度は高めになっており、一見すると違う解き方をしないといけないと感じる問題も含まれています。演習問題まできっちりと仕上げられれば、旧帝大や早慶といった難関大学の入試問題に太刀打ちできるようになります。 - (超)ミニ講座
より発展的な問題に対応していくために必要とされる手法や解法についての詳しい解説がなされています。 - コラム
より深い思考力を得るのに必要となる関連知識の深掘りができるようになっています。
『1対1対応の演習』の問題数とレベル
無理なく入試標準~応用レベルの実力をみにつけられる問題数
『1対1対応の演習』は、「大学入試で必要とされる数学力の土台」を効率よく固めるために厳選された問題がそろっています。問題数は以下の表のとおりです。
数学Ⅰ
| 単元 | 例題 | 演習題 | 合計 |
|---|---|---|---|
| 数と式 | 12 | 12 | 24 |
| 2次関数 | 20 | 20 | 40 |
| 集合と論理 | 8 | 8 | 16 |
| 図形と計量 | 10 | 10 | 20 |
| データの分析 | 6 | 6 | 12 |
| ミニ講座・コラム | 10 | – | 10 |
| 合計 | 66 | 56 | 122 |
数学Ⅱ
| 単元 | 例題 | 演習題 | 合計 |
|---|---|---|---|
| 式と証明 | 16 | 16 | 32 |
| 複素数と方程式 | 8 | 8 | 16 |
| 指数・対数・ 三角関数 | 15 | 15 | 30 |
| 座標 | 19 | 19 | 38 |
| 微分法とその応用 | 11 | 11 | 22 |
| 積分法とその応用 | 14 | 14 | 28 |
| ミニ講座・コラム | 7 | – | 7 |
| 合計 | 90 | 83 | 173 |
数学Ⅲ
| 単元 | 例題 | 演習題 | 合計 |
|---|---|---|---|
| 極限 | 14 | 14 | 28 |
| 微分法とその応用 | 18 | 18 | 36 |
| 積分法(数式) | 18 | 18 | 36 |
| 積分法(面積) | 12 | 12 | 24 |
| 積分法 (体積・弧長) | 13 | 13 | 26 |
| ミニ講座・コラム | 10 | – | 10 |
| 合計 | 85 | 75 | 160 |
数学A
| 単元 | 例題 | 演習題 | 合計 |
|---|---|---|---|
| 場合の数 | 12 | 12 | 24 |
| 確率 | 14 | 14 | 28 |
| 整数 | 18 | 18 | 36 |
| 図形の性質 | 12 | 12 | 24 |
| ミニ講座・コラム | 19 | – | 19 |
| 合計 | 75 | 56 | 131 |
数学B
| 単元 | 例題 | 演習題 | 合計 |
|---|---|---|---|
| 数列 | 16 | 16 | 32 |
| 統計的な推測 | 9 | 9 | 18 |
| 融合問題(ⅠAⅡB) | 19 | 19 | 38 |
| ミニ講座・コラム | 8 | – | 8 |
| 合計 | 52 | 44 | 96 |
数学C
| 単元 | 例題 | 演習題 | 合計 |
|---|---|---|---|
| ベクトル | 25 | 25 | 50 |
| 2次曲線 | 8 | 8 | 16 |
| いろいろな関数・曲線 | 8 | 8 | 16 |
| 複素数平面 | 14 | 14 | 28 |
| 数ⅢC総合問題 | 6 | 20 | 26 |
| ミニ講座・コラム | 4 | – | 4 |
| 合計 | 65 | 75 | 140 |
| 文系合計 ⅠAⅡB+ベクトル | 572 |
| 理系合計 ⅠAⅡBⅢC | 822 |
これらの無駄のない問題により、典型的な入試問題を通して中堅国公立大やMARCH、関関同立から早慶や旧帝大といった難関大学にまで対応できる解法パターンを体系的に学ぶことが可能になっています。
よく比較される『青チャート』『問題精講シリーズ』と比べると
| 参考書シリーズ | 文系問題数 | 理系問題数 |
|---|---|---|
| 青チャート(例題+練習問題) | 1,412題 | 2,200題 |
| 基礎問題精講+標準問題精講 | 1,341題 | 1,926題 |
| プレ1対1対応の演習+数学ⅢCの入試基礎+1対1対応の演習 | 1,241題 | 1,673題 |
となります。
青チャートや問題精講シリーズと比べて、より厳選された少ない問題数で効率よく学習できることがわかります。その分、使い方を間違えると学習効果が下がりやすいという事なので気を付けてください。
難関大入試の典型問題への対応力を定着させる
『1対1対応の演習』の目標は、「難関大レベルの問題を解くための足固め」とされています。これはより一般的な指標で考えると「入試標準~応用レベルの典型問題をきっちり解ける力をみにつける」といいかえられます。
この目標を効率的に達成できるように、『1対1』では受験数学のエッセンスを基本概念と結びつけ、体系的かつ効率的にスッキリとみにつけることができるように工夫されています。
注意点は、入試基礎レベルの内容は理解できていることが前提であることです。基礎レベルに不安がある場合には、無理して本書に取り組むべきではありません。『プレ1対1対応の演習』や『入門問題精講』に戻って、基礎を固めなおすことを優先しましょう。
掲載されている問題のレベルは「青チャートの🧭4つ以上の例題やExercise」と同等と考えてください。 標準問題精講で比較すると、「標準問題精講ⅠA≦1対1対応の演習」、「標準問題精講ⅡB+ベクトル≒1対1対応の演習」「1対1対応の演習≦標準問題精講ⅢC」となります。
『1対1対応の演習』の効果的な使い方
『1対1対応の演習』は、チャート式や問題精講シリーズのような、「入試に頻出で典型的な解法パターン(定石)を暗記する」ことが目標ではありません。
より少ない問題の中から、「幅広く応用の利く数学的な考え方」を効果的にみにつけていくことが目標です。ここでは、この目的を達成するためのおすすめの使い方を紹介します。
1周目の流れ
1周目のポイントは解法や考え方をじっくり理解することです。必要に応じて『プレ1対1対応の演習』や『入門問題精講』へ立ち返りつつ、スピードよりも質を重視して、確実に考え方をみにつけていってください。
- 要点の整理を確認する
まずは、基本知識にぬけがないか確認するために要点の整理に目を通しましょう。
ここで、「言ってる意味が分からない」とか「知らないことが半分以上ある」というような場合には明らかに基礎力不足です。『プレ1対1対応の演習』や『入門問題精講』といった参考書に戻り、より基礎となる知識を入れなおしましょう。 - 例題を解く
単元のポイントが確認できたら、いよいよ問題に挑戦です。まずは、何も見ずに例題が解けるかチャレンジしましょう。解答時間の目安は最大20分と考えておくと時間効率がよくなります。また、5分考えても「全く方針もたたない」という場合には、前文を確認してみましょう。
解き終わったら、前文・解答・傍注をしっかりと読み込んでください。間違っても、「答えがあっていたからOK~」と読み飛ばすようなことがないようにしましょう。たとえ正解していたとしても、もっとスマートな解法がなかったのかや、その問題にしか使えない解法になっていないかをじっくり考えることで、数学的な視野が広がります。
じっくり解答を確認したうえで、
正解でき、解答と同じレベルのすっきりした答案が作れていた 〇
正解できていて考え方もあっていたが、答案がスマートではなかった △
間違っていた、正解はしていたがほかの問題にも応用できるような考え方ではなかった、前文をみたからできた ×
のように、自分の到達度に応じて段階的に印をつけてください。 - 間違った問題を自分のものにする
2.で〇が付かなかった例題について、何も見ずに答案を再現できるか確認してください。このときに、「覚えて再現する」となってしまわないように注意しましょう。解答からきちんと「考え方」を吸収できていれば、丸暗記などせずとも答案を再現できます。 - 演習題を解く
例題で習得した考え方を実践できるかを確認します。例題に正面から取り組めていれば、例題は解けなくても演習題は解けたという事も出てくるはずです。
例題と同じ要領で取り組むことが重要です。(演習題には前文はついていません。手も足も出ないという場合には、例題を参考にしましょう。)
1周目では解ける問題のほうが少ないと思います。これは誰でも(東大合格者であっても)同じなので、気にする必要は全くありません。初めからは解けないのが当たり前です。
「この問題」を解くための知識は、単なる丸暗記です。これではほかの問題には応用できず、貴重な記憶領域の無駄遣いです。一つの問題を通して、いかに応用性の高い考え方ができるようになるかが重要です。確かにこれは簡単ではありませんが、自分なりに「このタイプの問題はこう解けばいいのでは?」と、攻略方法を探ることを習慣化していきましょう。
2周目以降の流れ
2周目以降の目的は1周目で学んだ考え方を、自分の自然な思考プロセスとなるように馴染ませていくことです。大学入試という「制限時間内に自分の考えを会ったこともない他人に正しく伝えるゲーム」をクリアするために、時間にも意識を向けて取り組んでください。
- 1周目のときに〇のつかなかった例題に取り組む
1周目のときと同様に、例題を解き進めてください。
制限時間の目安は15分です。このとき、〇のついている問題は頭の中で解答再現するだけでも構いません。
演習題は旧帝大や早慶といった難関大志望者のみ取り組んでください。それ以外の人については、例題レベルを100%解ける状態にすることに一旦集中しましょう。 - 一段階高いレベルの問題で実際に使えるように練習する。
7~8割の例題(難関大志望者は演習題も)に制限時間内に正答できるようになったら、演習題(難関大志望者は『新数学スタンダード演習』『数学ⅢCスタンダード演習』))で実際に使えるか確認しましょう。
例題については、『1対1』の解答に至る思考プロセスを100%自分のものにできるまで周回してください。このときに、「正解できたか」だけで判断してはいけません。また、解法の丸暗記にならないようにも注意して取り組みましょう。
中堅国公立大学やGMARCH、関関同立志望者についてはこの段階で実際に過去問に挑戦してみるのも効果的です。
『1対1対応の演習』を進める目的は、「幅広く応用の利く数学的な考え方」をみにつけることです。入試で初見の問題に対応できるかどうかは、「この考えとこの考えをこう組み合わせていけば解ける」と、思考をつなげていけるかどうかが重要です。解法がきちんと説明できる(正しい考え方が定着している)状態になれば、しぜんと正解できるようになっています。
どんな人に『1対1対応の演習』はおすすめ?
『大学への数学 1対1対応の演習』は選び抜かれた入試標準~応用レベルの問題を通して、幅広く応用の利く数学的思考を身につけられます。解説も丁寧かつシンプルで、難関大入試に挑戦する準備を効率よく進められます。
そのため、受験で数学を使う多くの人におすすめできます。ここでは、『1対1』がオススメの人を具体的にみていきます。
『1対1対応の演習』がオススメの人
中堅国公立大学やGMARCH、関関同立レベルの大学が志望の人
このレベルの人がやるべきことは、標準レベルの問題を確実に解ききれるようになることです。
そのため、受験で頻出する標準レベルの解法や思考方法を無駄なく学べる『1対1対応の演習』は非常にオススメです。
例題を中心に、じっくりと数学的な考え方を自分のものとしていくことで、得点力を安定させることができます。演習題まで取り組めば、数学を得点源にすることも十分に可能になります。
難関大学が(旧帝大や早慶上理など)志望の人
難関大学を目指す受験生にとって、『1対1対応の演習』はほぼ必須といえるくらいにオススメです。
難関大学の入試で頻出かつ取りこぼせないテーマが厳選されており、効率よく難関大の求める思考力を鍛えることができます。
『1対1』を終えたら過去問に挑戦してみてください。難しいと思っていた入試問題に、意外とすんなりと取り組めるはずです。
東大・京大・一橋大・東京科学大などの最難関大学が志望の人
このレベルの大学を目指す場合、『1対1対応の演習』で得られる考え方は、身についていて当然と考えましょう。
チャート式や問題精講シリーズなどでいくらパターンを増やしても、それだけでは全く入試では通用しません。
『1対1』で問題への正しいアプローチ方法を高2のできるだけ早い段階でみにつけ、『スタ演』などにより複雑に絡み合った入試問題を紐解くトレーニングを積んでください。
あまりおすすめでない人
『大学への数学 1対1対応の演習』は、基礎が十分に固まっていない人や、基礎レベル徹底が重要な地方国公立大学や日東駒専、産近甲龍といった私立大学を志望する人には、あまりお勧めできません。
『1対1対応の演習』は、基礎が整った状態で入試標準~応用レベルの問題に取り組むことを想定しています。基礎が不確かな状態では使いこなすことはできません。『1対1』を効果的に活用するには問題の本質的な理解大切ですが、基礎が固まっていないとそれが困難です。結果として、「解法をただ暗記することに時間を費やしてしまう」ことになります。
また、志望校が日東駒専・産近甲龍レベルの場合、『1対1対応の演習』の内容はオーバーワークです。無理をして手を出すべきではありません。『入試数学の基礎徹底』『数学ⅢCの入試基礎』『プレ1対1対応の演習』といった入試基礎レベルを固める参考書で基礎レベルの理解を深めることを優先しましょう。
『1対1対応の演習』の次に取り組むべき参考書
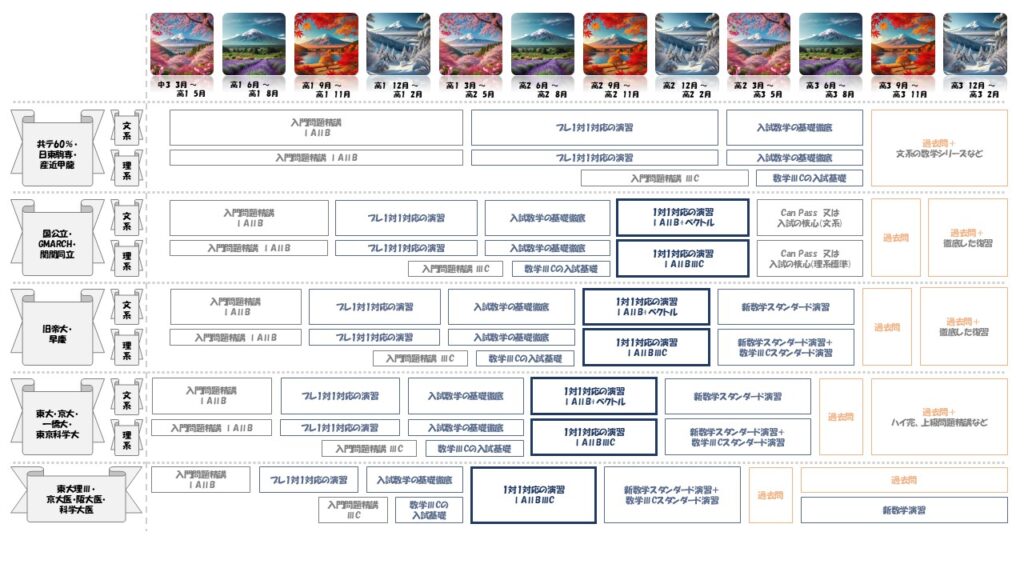
ここでは、『1対1対応の演習』に取り組むべき時期と、『1対1』が仕上がった後に何を進めていくべきかを志望校別に紹介します。
本来、一人一人の状況で全く変わってしまう参考書の選び方ですが、これまでの経験から「失敗しにくい一例」として参考書学習のルートをいくつか紹介していきます。よければ参考にしてください。
理系向け:志望校レベル別おすすめ参考書
GMARCH・関関同立・中堅国公立大学志望の人
このレベルが志望の場合、入試標準レベルの問題の演習をいかに効果的に積み上げるかがポイントになります。
標準レベルの問題を確実に解ききる力を身につけ、余裕があれば、応用問題に少し触れておくといいですね。
- Stage 1~高2の5月
高校入学後なるべく早い段階から、入門レベルの学習に取り組みましょう。遅くとも高2の5月には数学ⅢCまでの範囲学習を一通り終えることが目標です。
- Stage 2高2の6月~9月
この期間で、『入試数学の基礎徹底』『数学ⅢCの入試基礎』に取り組み、入試基礎レベルを仕上げてください。
並行して『合格る計算』などで計算練習をこなしておくことも重要です。
- Stage 3高2の10月~3月
高2の間に『1対1対応の演習』を数学ⅠAⅡBCⅢの全範囲について完成させることを目標に、十分な時間をかけて取り組む期間にしてください。『1対1』をいかにきっちり仕上げることができるかで今後の学習効率が大きく変わります。
- Stage 4高3の4月~8月
『CanPass』や『理系数学入試の核心(標準編)』といった演習書で実践練習を進めるようにしてください。
少しでも不安な時はすぐに『1対1対応の演習』などに戻って復習するように徹底しましょう。
遅くとも9月からは志望校の過去問に取り組めるように進めていくことが重要です。
共通テスト受験者は、少しずつ共通テストの過去問に取り組み、共通テスト対策を進めるのも忘れてはいけません。
- Stage 5高3の9月~入試本番
過去問演習に全力で取り組む時期です。過去問を通して見つかった弱点分野については、これまでに使ってきた参考書の徹底した復習で補強を進めてください。
これらを通して、入試標準レベルの問題に対する解答力を磨き上げていってください。
1対1対応の演習→理系数学入試の核心(標準編)やCan Pass(Can Passは国公立志望のみ)→過去問
難関大学(旧帝大・早慶上理)志望の人
最難関私立や難関国公立を目指す人には、入試標準から応用レベルの問題を徹底して演習することが必要です。そのため、以下のようなルートがおすすめです。
- Stage 1~高1の3月
高校入学後なるべく早い段階から、入門レベルの学習に取り組みましょう。遅くとも高1の3月中には数学ⅢCまでの範囲学習を一通り終えるようにしましょう。
- Stage 2高2の4月~8月
この期間で、『入試数学の基礎徹底』『数学ⅢCの入試基礎』に取り組み、入試基礎レベルを仕上げてください。
並行して『合格る計算』などで計算練習をこなしておくことも重要です。
- Stage 3高2の9月~2月
高2の春休みまでに『1対1対応の演習』を数学ⅠAⅡBCⅢの全範囲について完成させることをが目標になります。限られた期間ですが、十分な時間をかけて取り組むようにしてください。『1対1』をいかにきっちり仕上げることができるかで今後の学習効率が大きく変わります。
- Stage 4高2の3月~高3の8月
『新数学スタンダード演習』や『数学ⅢCスタンダード演習』といった応用レベルを手厚くカバーできる演習書で実践練習を進めるようにしてください。
少しでも不安な時はすぐに『1対1対応の演習』などに戻って復習するように徹底しましょう。
3月中に1度は過去問に触れておき、「どれくらいのレベルに到達しなければならないか」を知ったうえで演習量を稼いでください。9月からは本格的に志望校の過去問に取り組めるように進めていくことが重要です。
共通テスト受験者は、少しずつ共通テストの過去問に取り組み、共通テスト対策を進めるのも忘れてはいけません。
- Stage 5高3の9月~入試本番
過去問演習に全力で取り組む時期です。過去問を通して見つかった弱点分野については、これまでに使ってきた参考書の徹底した復習で補強を進めてください。
『1対1』の後は、同じ大数シリーズの『スタ演(ⅢCも含む)』に進むのが効率的で最もオススメです。
本番までの残り時間を考えたときに、どうしても問題数を絞る必要があるなら『理系数学入試の核心(標準編)』や『やさしい理系数学』を使うのもありです。
演習を進める中で時間配分や解答スピードを意識し、試験本番でも通用する対応力をみにつけてください。
1対1対応の演習→新数学スタンダード演習+数学ⅢCスタンダード演習→過去問
最難関大学(東大・京大・東京科学大)志望の人
最難関大学を目指す場合には、入試標準レベルを固めたうえで、さらに高度な応用力を身につけることが必要です。
最終的には『上級問題精講』や『新数学演習』『ハイレベル理系数学』といった問題集を活用し、深い思考を要する問題への対応力をみにつけてください。
- Stage 1~高1の12月
高校入学後なるべく早い段階から、入門レベルの学習に取り組みましょう。遅くとも高1の12月中には数学ⅢCまでの範囲学習を一通り終えるようにしましょう。
- Stage 2高1の1月~高2の6月
この期間で、『入試数学の基礎徹底』『数学ⅢCの入試基礎』に取り組み、入試基礎レベルを仕上げてください。
並行して『合格る計算』などで計算練習をこなしておくことも重要です。
- Stage 3高2の7月~12月
高2の冬休みまでに『1対1対応の演習』を数学ⅠAⅡBCⅢの全範囲について完成させることをが目標になります。限られた期間ですが、十分な時間をかけて取り組むようにしてください。『1対1』をいかにきっちり仕上げることができるかで今後の学習効率が大きく変わります。
- Stage 4高2の1月~高3の6月
『新数学スタンダード演習』や『数学ⅢCスタンダード演習』といった応用レベルを手厚くカバーできる演習書で実践練習を進めるようにしてください。
少しでも不安な時はすぐに『1対1対応の演習』などに戻って復習するように徹底しましょう。
3月中に1度は過去問に触れておき、「どれくらいのレベルに到達しなければならないか」を知ったうえで演習量を稼いでください。7月(夏休み)からは本格的に志望校の過去問に取り組めるように進めていくことが重要です。
共通テスト受験者は、少しずつ共通テストの過去問に取り組み、共通テスト対策を進めるのも忘れてはいけません。
- Stage 5高3の夏休み
過去問演習に全力で取り組む時期です。過去問を通して敵のレベルや自分の弱点を明確化していきましょう。見つかった弱点分野については、これまでに使ってきた参考書の徹底した復習で補強を進めてください。
※共通テストは決して簡単な試験ではありません。個別試験の過去問だけでなく、共通テストの過去問にもきちんと取り組みましょう。
- Stage 6高3の9月~入試本番
当然、過去問演習を継続していく期間です。必要に応じて、『新数学演習』『上級問題精講』『ハイレベル数学の完全攻略』などを並行して進めてください。
1対1対応の演習→新数学スタンダード演習+数学ⅢCスタンダード演習→過去問→過去問+新数学演習/上級問題精講/ハイレベル数学の完全攻略
このルートでいければ、柔軟な思考力が求められる東大・京大レベルの問題にも確実に対応できる実力が身につきます。『スタ演(ⅢC含む)』の後は、一旦過去問演習を挟み、必要に応じて『新数演』などに取り組めるといいでしょう。
※東大理Ⅲ、京大医など最難関医学部志望の場合は『新数演』も必須です。高3の4月から過去問演習に手を付けることができるように、上記よりも約2ヶ月前倒しで学習を進めるように意識してください。入試基礎レベルまでを高1の間に終わらせるようなイメージで取り組めると理想的です。
文系向け:志望校レベル別おすすめ参考書
GMARCH・関関同立・中堅国公立大学志望の人
このレベルを志望する文系の人は、頻出問題を中心に実戦力をつけるのが効果的です。
『文系の数学(重要事項完全習得編/実戦力向上編)』や『Can Pass』などを使って、よく出題されるパターンや標準的な問題に対応できるようにしましょう。
- Stage 1~高2の5月
高校入学後なるべく早い段階から、入門レベルの学習に取り組みましょう。遅くとも高2の5月には範囲学習を一通り終えることが目標です。
- Stage 2高2の6月~9月
この期間で、『入試数学の基礎徹底』に取り組み、入試基礎レベルを仕上げてください。
並行して『合格る計算』などで計算練習をこなしておくことも重要です。
- Stage 3高2の10月~3月
高2の間に『1対1対応の演習』を数学ⅠAⅡBCの全範囲について完成させることを目標に、十分な時間をかけて取り組む期間にしてください。『1対1』をいかにきっちり仕上げることができるかで今後の学習効率が大きく変わります。
- Stage 4高3の4月~8月
『CanPass』や『文系の数学(重要事項完全習得編/実戦力向上編)』といった演習書で実践練習を進めるようにしてください。
少しでも不安な時はすぐに『1対1対応の演習』などに戻って復習するように徹底しましょう。
遅くとも9月からは志望校の過去問に取り組めるように進めていくことが重要です。
共通テスト受験者は、少しずつ共通テストの過去問に取り組み、共通テスト対策を進めるのも忘れてはいけません。
- Stage 5高3の9月~入試本番
過去問演習に全力で取り組む時期です。過去問を通して見つかった弱点分野については、これまでに使ってきた参考書の徹底した復習で補強を進めてください。
1対1対応の演習→文系の数学(重要事項完全習得編/実戦力向上編)→Can Pass(Can Passは国公立志望のみ)→過去問
難関大学(早慶上理・難関国公立)志望の人
標準問題に慣れたうえで、応用問題にも対応する力が必要です。同じ大数シリーズの『スタ演』に進み、文系数学の応用問題に慣れるようにしましょう。
入試で頻出のパターンをしっかり押さえ、解答スピードを意識しながら演習することで、得点力を磨き上げてください。
- Stage 1~高1の3月
高校入学後なるべく早い段階から、入門レベルの学習に取り組みましょう。遅くとも高1の3月中には範囲学習を一通り終えるようにしましょう。
- Stage 2高2の4月~8月
この期間で、『入試数学の基礎徹底』に取り組み、入試基礎レベルを仕上げてください。
並行して『合格る計算』などで計算練習をこなしておくことも重要です。
- Stage 3高2の9月~2月
高2の春休みまでに『1対1対応の演習』を数学ⅠAⅡBCの全範囲について完成させることをが目標になります。限られた期間ですが、十分な時間をかけて取り組むようにしてください。『1対1』をいかにきっちり仕上げることができるかで今後の学習効率が大きく変わります。
- Stage 4高2の3月~高3の8月
『新数学スタンダード演習』のような応用レベルを手厚くカバーできる演習書で実践練習を進めるようにしてください。
少しでも不安な時はすぐに『1対1対応の演習』などに戻って復習するように徹底しましょう。
3月中に1度は過去問に触れておき、「どれくらいのレベルに到達しなければならないか」を知ったうえで演習量を稼いでください。9月からは本格的に志望校の過去問に取り組めるように進めていくことが重要です。
共通テスト受験者は、少しずつ共通テストの過去問に取り組み、共通テスト対策を進めるのも忘れてはいけません。
- Stage 5高3の9月~入試本番
過去問演習に全力で取り組む時期です。過去問を通して見つかった弱点分野については、これまでに使ってきた参考書の徹底した復習で補強を進めてください。
1対1対応の演習→新数学スタンダード演習→過去問
最難関大学(東大・京大・一橋大)志望の人
最難関大学を目指す場合には、基礎から標準を固めたうえで、さらに高度な応用力をつけることが求められます。
最終的には『文系数学の良問プラチカ』『上級問題精講』『ハイレベル数学完全攻略』といったハイレベルな問題集を活用し、対応力をみにつけられると理想的です。
- Stage 1~高1の12月
高校入学後なるべく早い段階から、入門レベルの学習に取り組みましょう。遅くとも高1の12月中には範囲学習を一通り終えるようにしましょう。
- Stage 2高1の1月~高2の6月
この期間で、『入試数学の基礎徹底』に取り組み、入試基礎レベルを仕上げてください。
並行して『合格る計算』などで計算練習をこなしておくことも重要です。
- Stage 3高2の7月~12月
高2の冬休みまでに『1対1対応の演習』を数学ⅠAⅡBCの全範囲について完成させることをが目標になります。限られた期間ですが、十分な時間をかけて取り組むようにしてください。『1対1』をいかにきっちり仕上げることができるかで今後の学習効率が大きく変わります。
- Stage 4高2の1月~高3の6月
『新数学スタンダード演習』のような応用レベルを手厚くカバーできる演習書で実践練習を進めるようにしてください。
少しでも不安な時はすぐに『1対1対応の演習』などに戻って復習するように徹底しましょう。
3月中に1度は過去問に触れておき、「どれくらいのレベルに到達しなければならないか」を知ったうえで演習量を稼いでください。7月(夏休み)からは本格的に志望校の過去問に取り組めるように進めていくことが重要です。
共通テスト受験者は、少しずつ共通テストの過去問に取り組み、共通テスト対策を進めるのも忘れてはいけません。
- Stage 5高3の夏休み
過去問演習に全力で取り組む時期です。過去問を通して敵のレベルや自分の弱点を明確化していきましょう。見つかった弱点分野については、これまでに使ってきた参考書の徹底した復習で補強を進めてください。
※共通テストは決して簡単な試験ではありません。個別試験の過去問だけでなく、共通テストの過去問にもきちんと取り組みましょう。
- Stage 6高3の9月~入試本番
当然、過去問演習を継続していく期間です。必要に応じて、『文系数学の良問プラチカ』『上級問題精講』『ハイレベル数学完全攻略』などを並行して進めてください。
1対1対応の演習→新数学スタンダード演習→過去問→過去問+文系数学の良問プラチカ/上級問題精講/ハイレベル数学完全攻略
※『スタ演』の後は一旦過去問演習です。過去問に実際に触れてみて、必要性を感じた場合のみさらにハイレベルな問題演習に時間を使うようにしてください。
『1対1対応の演習』まとめと活用の極意
『大学への数学 1対1対応の演習』は、受験数学において多くの受験生から支持される参考書です。特に、GMARCHや旧帝大、早慶といった中堅から難関大学を志望する人にとって、効率的に入試問題を解く力を身につけることができる実用性の高いシリーズといえます。
『1対1』の大きな特長は、問題が厳選されている点です。青チャートのように膨大な問題をこなすスタイルではなく、入試に必要な典型問題を中心に効率的に学べる構成が魅力です。無駄を削ぎ落とした問題選定により、少ない問題数でも効果的に実力を伸ばすことができます。また、例題と演習題が1対1で対応していることで、理解した解法を次の段階で実際に使いこなす練習ができ、ただ解法を暗記するのではなく、考える力を身につけることが可能です。
効果的な使い方として、まず1周目では「理解すること」を最優先してください。例題に取り組み、解答に詰まった場合には前文をしっかり読み込み、問題の意図や解法の流れを掴みます。解説を確認しながら、答えを合わせるだけで終わらせるのではなく、なぜその解法が有効なのかをじっくり考えることが大切です。そして、2周目以降は演習題を中心に取り組みながら、時間を意識した実戦的な練習を行います。このプロセスを繰り返すことで、受験本番で求められる「限られた時間で解答を仕上げる力」を身につけることができるでしょう。
ただし、『1対1対応の演習』は基礎力が整っている人を対象としています。基礎問題でつまずく段階の人には難易度が高いため、無理に取り組むのは避けるようにしてください。基礎が不十分な場合は、まず『プレ1対1対応の演習』などで基礎力を固めてから挑戦するようにしましょう。基礎が整っていない状態で取り組むんでも、効果を最大限に引き出すことが難しく、時間の無駄使いになります。
難関といわれる大学を志望する場合には、『1対1』を終えた後の学習の進め方も重要になります。『新数学スタンダード演習』や『数学ⅢCスタンダード演習』へのステップアップにより、実践的な問題演習を積み重ねるのが有効です。最難関大学を目指す場合には、『新数学演習』や『上級問題精講』を取り入れることで応用力を磨くとよいでしょう。
『1対1対応の演習』は、効率的に数学力を伸ばすための強力な味方です。基礎が整ったうえで『1対1』を最後まで仕上げることができれば、大学入試の数学で求められる思考力を十分に身につけることができます。志望校合格への道を切り開くために、ぜひ活用してみてください。






コメント