連立1次不等式

連立1次不等式

中学で学習した連立方程式と似た名前であるが、解き方は異なる。
連立方程式では、2式を足したり引いたりすることで値を求めたが、連立不等式ではそれぞれの不等式を解いた共通範囲が解となる。

共通範囲を考えるときには、数直線上に図示して考えるのが確実である。図示する際には、

1．条件（各範囲）ごとに高さを変える
2．端（その数）を含む場合は黒丸 / 端（その数）を含まない場合は白丸
3．端（その数）を含む場合は直角に立ち上げる / 端（その数）を含まない場合は斜めに立ち上げる

というルールになっている。
※実際に回答するときには、3つ目はそこまで気にしなくても問題ない。しかし、一見してのわかりやすさなどを考えると、かき分ける癖をつけておく方がよい。

例題に挑戦しよう

≪問題≫

次の不等式を解け。
(1) $\begin{eqnarray} \left\{ \begin{array}{l} 5x-2\gt 6x-7\\ x-15\leqq 3-2x \end{array} \right. \end{eqnarray}$

(2) $\begin{eqnarray} \left\{ \begin{array}{l} 4x-1\lt 2x-5\\ 2x+2\geqq 3-x \end{array} \right. \end{eqnarray}$

(3) $2x-5\lt 7x-5\lt -3x+7$

≪解答・解説≫

(1)
$\begin{eqnarray} 5x-2&\gt&6x-7\\ 5x-6x&\gt&-7+2\\ -x&\gt&-5\\ x&\lt&5\qquad\cdots\cdots➀ \end{eqnarray}$

$\begin{eqnarray} x-15&\leqq&3-2x\\ x+2x&\leqq&3+15\\ 3x&\leqq&18\\ x&\leqq&6\qquad\cdots\cdots➁ \end{eqnarray}$

$\therefore$　➀,➁の共通範囲より $\boldsymbol{x\lt 5}$

(2)
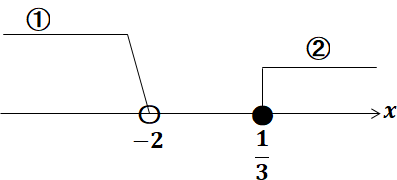
$\begin{eqnarray} 4x-1&\lt&2x-5\\ 4x-2x&\lt&-5+1\\ 2x&\lt&-4\\ x&\lt&-2\qquad\cdots\cdots➀ \end{eqnarray}$

$\begin{eqnarray} 2x+2&\geqq&3-x\\ 2x+x&\geqq&3-2\\ 3x&\geqq&1\\ x&\geqq&\dfrac{1}{3}\qquad\cdots\cdots➁ \end{eqnarray}$

$\therefore$　➀,➁の共通範囲は存在しないので、 解なし

(3)※$A\lt B\lt C$ は、$A\lt B$, $B\lt C$ に分けて考える。
$2x-5\lt 7x-5\lt -3x+7$より、
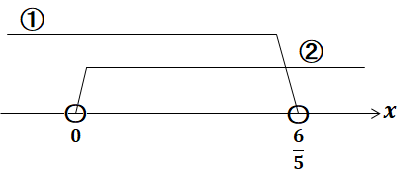
$\begin{eqnarray} 2x-5&\lt&7x-5\\ 2x-7x&\lt&-5+5\\ -5x&\lt&0\\ x&\gt&0\qquad\cdots\cdots➀ \end{eqnarray}$

$\begin{eqnarray} 7x-5&\lt&-3x+7\\ 7x+3x&\lt&7+5\\ 10x&\lt&12\\ x&\lt&\dfrac{6}{5}\qquad\cdots\cdots➁ \end{eqnarray}$

$\therefore$　➀,➁の共通範囲より $\boldsymbol{0\lt x\lt\dfrac{6}{5}}$